Diagnostische Tests

Seitenübersicht

Einführung
Diagnostische Kenngrößen
Gütebewertung diagnostischer Tests
- ROC-Kurve

Einführung

Ein diagnostischer Test ist eine Methode, um auf Basis einer oder mehrerer vorliegender Parameter zu entscheiden, ob eine betrachtete Versuchsperson an einer bestimmten Krankheit erkrankt ist oder nicht. Es muss sich in der Praxis nicht unbedingt um eine Krankheit handeln, da z. B. ein Schwangerschaftstest auch ein diagnostischer Test ist oder ein Staging zwischen gut- und bösartigen Tumoren unterscheiden kann. Trotzdem sprechen wir der Einfachheit halber im Folgenden von krank versus gesund. Es geht also darum, eine Diagnose zu stellen. Diagnosestudien haben das Ziel, die Güte eines diagnostischen Verfahrens, wie z. B. eines diagnostischen Tests zu bewerten. Dabei werden verschiedene Gütekriterien wie die Reliabilität und die Validität zu Rate gezogen. Die Reliabilität betrachtet, inwiefern bei Wiederholung des Tests unter gleichen Bedingungen auch die gleichen Testergebnisse erzeugt werden (wir werden im Rahmen des EpiBioManuals nicht weiter darauf eingehen, mehr Informationen findest du in Kapitel 14.1.4 in Weiß 2013). Die Validität beschreibt, inwiefern es dem Test gelingt, zwischen gesunden und kranken Personen zu unterscheiden. Sie wird mithilfe der Sensitivität und Spezifität bestimmt, die unter anderem im weiteren Verlauf dieses Kapitels thematisiert werden.

Ein diagnostischer Test wird an der Versuchsperson durchgeführt und hat zwei mögliche Ergebnisse: positiv oder negativ (ungültige Ergebnisse werden nicht betrachtet). Ist der Test korrekt, dann bedeutet ein positives Ergebnis, dass die Versuchsperson als erkrankt eigestuft wird und ein negatives Ergebnis, dass sie als gesund eingestuft wird. In der Praxis kommen allerdings auch manchmal falsche Testergebnisse vor: Es kann entweder sein, dass die Versuchsperson in Wahrheit erkrankt ist, der Test dies allerdings „übersieht“ und negativ ist (falsch negativ). Der zweite mögliche Testfehler tritt auf, wenn der Test von einer Krankheit ausgeht, also positiv ist, die Versuchsperson in Wirklichkeit aber gesund ist (falsch positiv). Hierfür muss für jede Versuchsperson daher auch noch ein sogenannter Goldstandard oder Referenzstandard erhoben werden, der die Wahrheit definiert und entsprechend die zuverlässigste zur Verfügung stehende Methode sein sollte. Die vier möglichen Testergebnisse lassen sich übersichtlich in einer diagnostischen Vierfeldertafel (Tab. 1) darstellen, die in den Spalten den wahreren Krankheitszustand (Goldstandard) und in den Zeilen das Testergebnis beschreibt.

Tab. 1: Diagnostische Vierfeldertafel
	Krank $D^+$	Gesund $D^-$	Gesamt
Test positiv $T^+$	$a$ : richtig positiv	$b$ : falsch positiv	$a+b$
Test negativ $T^-$	$c$ : falsch negativ	$d$ : richtig negativ	$c+d$
Gesamt	$a+c$	$b+d$	$n$

Beispiel "Blutdrucksenker"

Ab einem dauerhaft anhaltenden systolischen Blutdruckwert von 140 mmHg oder höher wird von einer Hypertonie gesprochen. Durch regelmäßige Blutdruckmessungen gilt es, die Erkrankung aufzudecken. Für unsere beispielhafte Interventionsstudie zur Wirkung eines neuen Blutdruck senkenden Medikaments sollen im weiteren Verlauf des EpiBioManuals 100 Testpersonen mit einer Hypertonie untersucht werden. Vorab wird in der hier thematisierten Diagnosestudie überprüft, ob eine Hypertonie vorliegt. Es wird vorerst bei 1000 Patient:innen eine Untersuchung auf Bluthochdruck durchgeführt, um dann später aus den Personen, die tatsächlich an einer Hypertonie leiden, 100 geeignete Studienteilnehmer:innen für die Interventionsstudie auszuwählen (wobei die Eignung anhand weiterer Einschlusskriterien und Ausschlusskriterien definiert wird). Die gemessenen Blutdruckwerte hängen von sehr vielfältigen Faktoren wie der Tageszeit, der momentanen emotionalen und körperlichen Verfassung oder schlichtweg der Erwartungsangst des/der Patient:in ab. Es finden sich Studien, die berichten, dass die Messergebnisse der ersten Blutdruckmessung häufig höhere Ergebnisse als den tatsächlichen Blutdruck des/der Patient:in liefern. Daher stellt sich die Frage, ob mit einer einzelnen Messung (die erste Messung) ein Bluthochdruck zuverlässig diagnostiziert werden kann. Dann kann man für dieses Beispiel eine Vierfeldertafel (Tab. 2) mit den Ergebnissen der ersten Blutdruckmessung (Zeilen) und dem wahren Zustand der Patient:innen, also dem Goldstandard (Spalten) betrachten:

Tab. 2:
	Hyperton $D^+$	Normoton $D^-$	Gesamt
1. Messung $>=$ 140 mmHg $T^+$	$a=250$	$b=140$	$a+b=390$
1. Messung $<$ 140 mmHg $T^-$	$c=20$	$d=590$	$c+d=610$
Gesamt	$a+c=270$	$b+d=730$	$n=1000$

Wir sehen, dass bei der ersten Messung bei 390 (

a+b

) von 1000 Patient:innen ein zu hoher Blutdruck festgestellt wurde, obwohl in Wirklichkeit nur 270 (

a+c

) Patient:innen der betrachteten Kohorte unter einer Hypertonie leiden. In lediglich 20 (

c

) Fällen haben die Tests noch nicht bei der ersten Messung, sondern erst nach wiederholter Messung die Diagnose Hypertonie ergeben (falsch-negativ). Hingegen gab es 140 Fälle (

b

), in denen die erste Messung zu falsch-positiven Ergebnissen geführt hat. Es wird dann vorerst von einem zu hohen Blutdruck ausgegangen, obwohl diese Patient:innen in Wahrheit gar keine Anzeichen einer Hypertonie aufweisen.¹

In der Praxis ist es oft der Fall, dass ein diagnostischer Test zwar als Ergebnis nur „positiv“ und „negativ“ anzeigt, dieses Ergebnis aber auf Basis eines konkreten Messwertes beruht, der einen spezifischen Grenzwert überschritten hat. In unserem Beispiel zum Blutdruck senkenden Medikament haben wir diesen Grenzwert, der eine gesunde von einer erkrankten Person unterscheidet, z. B. auf einen systolischen Blutdruck von 140 mmHg festgelegt. Es kommen meist verschiedene Grenzwerte infrage, die dann jeweils zu unterschiedlichen Ergebnissen in der als nächstes thematisierten Kenngrößen Sensitivität und Spezifität des Tests führen. Welcher Grenzwert am besten geeignet ist, kann mithilfe der ROC-Kurve bestimmt werden, die im weiteren Verlauf des Kapitels noch genauer erläutert wird.

Diagnostische Kenngrößen

Mithilfe der diagnostischen Vierfeldertafel können Kenngrößen berechnet werden, die die Aussagekraft des diagnostischen Tests betrachten. Dies ist sowohl von Interesse für die Testentwickler:innen selbst als auch für Ärzt:innen bzw. Patient:innen.

Sicht der Testentwickler:innen

Die Testentwickler:innen sind besonders interessiert daran, dass ihr Test wahrheitsgemäße Ergebnisse liefert. Sie prüfen ihre Tests, indem sie die Testergebnisse und die Ergebnisse des Goldstandards vergleichen. Die zwei Kenngrößen, die dabei eine große Rolle spielen, sind die Sensitivität und die Spezifität.

Die Sensitivität ist die Wahrscheinlichkeit, dass bei einer erkrankten Person, der Test auch tatsächlich positiv ausfällt. Es geht also um die Wahrscheinlichkeit eines positiven Tests unter der Bedingung, dass die Person erkrankt ist. Deshalb spricht man in diesem Fall von einer bedingten Wahrscheinlichkeit. Hat ein Test eine hohe Sensitivität, werden also die Erkrankten mit einer hohen Wahrscheinlichkeit anhand des Tests erkannt. Die Sensitivität berechnet sich aus der diagnostischen Vierfeldertafel wie folgt:

$P(T^+|D^+)=\frac{a}{a+c}.$

Es handelt sich also um den Anteil an den richtig positiven Testergebnissen an allen tatsächlich Erkrankten. Die Bedingung der Erkrankung $D^+$ ist in der obigen Formel hinter dem Strich dargestellt.

Die Spezifität hingegen beschreibt die Wahrscheinlichkeit, dass eine gesunde Testperson auch tatsächlich ein negatives Testergebnis aufweist, also den Anteil an richtig negativen Testergebnissen an allen Gesunden:

$P(T^-|D^-)=\frac{d}{b+d}.$

Sensitivität und Spezifität sollen bei einem guten diagnostischen Test also möglichst hohe Werte aufweisen.

Beispiel "Blutdrucksenker"

Wir wollen nun die Sensitivität und Spezifität für unser Beispiel berechnen. Als Erinnerung hier nochmal die Vierfeldertafel, aus der sich die gesuchten Werte ergeben.

Tab. 3:
	Hyperton $D^+$	Normoton $D^-$	Gesamt
1. Messung $>=$ 140 mmHg $T^+$	$a=250$	$b=140$	$a+b=390$
1. Messung $<$ 140 mmHg $T^-$	$c=20$	$d=590$	$c+d=610$
Gesamt	$a+c=270$	$b+d=730$	$n=1000$

Was sagen diese Werte nun aus? Die Wahrscheinlichkeit, dass bei einer Person, die tatsächlich unter Hypertonie leidet, die erste Blutdruckmessung auch einen systolischen Blutdruck über 140 mmHg angibt, liegt bei 93 % (Sensitivität). Hingegen ist die Wahrscheinlichkeit, dass eine normotone Person auch direkt bei der ersten Messung als gesund eingestuft wird (Blutdruck unter 140 mmHg) etwas geringer, nämlich bei 81 % (Spezifität). Baumdiagramme können hilfreich sein, Sachverhalte mit bedingten Wahrscheinlichkeiten übersichtlich darzustellen. Schaut euch die zwei zweistufigen Baumdiagramm zu unserem Beispiel an:

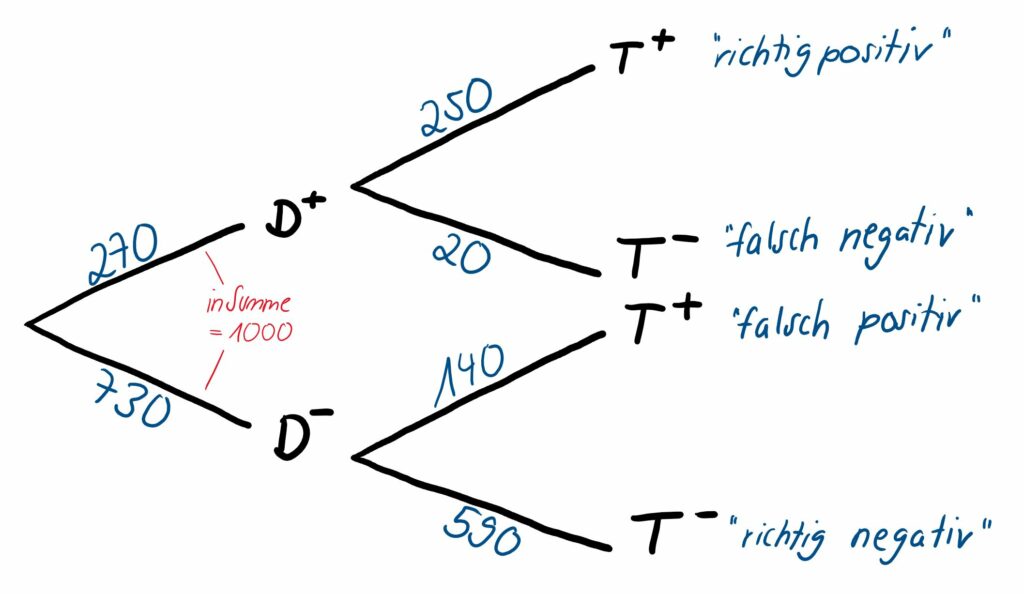
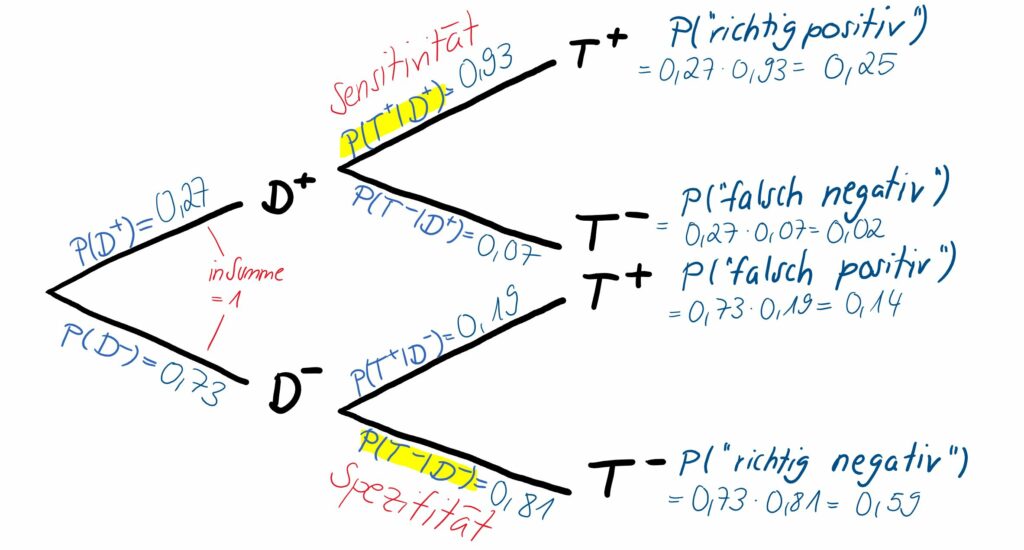
Wir wollen sowohl ein Baumdiagramm mit absoluten Häufigkeiten (Abb. 1) als auch eins mit den zugehörigen Wahrscheinlichkeiten (Abb. 2) betrachten. Welche Darstellungsart ihr bevorzugt, ist euch überlassen.

In schwarz ist die jeweilige Ausprägung der möglichen Ergebnisse angezeigt, also gehen wir bei einer mit Bluthochdruck erkrankten Person z. B. den oberen Pfad der ersten Abzweigung Richtung entlang. Wir wissen aus der ersten Spalte der Vierfeldertafel, dass 270 von den insgesamt 1000 Patient:innen hyperton sind. Somit beträgt die zugehörige einfache Wahrscheinlichkeit, dass eine Person an einer Hypertonie leidet, $P(D^+)=27 \%$ . Diese Wahrscheinlichkeit wird auch als Prävalenz (von lateinisch „praevalere“ = „vorherrschen“) der Erkrankung in der betrachteten Patient:innengruppe bezeichnet, auf die an späterer Stelle zu den Querschnittstudien noch genauer eingegangen wird. Umgekehrt sind 730 von 1000 (zweite Spalte der Vierfeldertafel), also 73 %, der Patient:innen normoton, was am unteren Pfad eingetragen wird. In Summe ergeben die zwei absoluten Werte 1000 und die zwei Wahrscheinlichkeiten immer 1.
Hat eine dieser erkrankten Personen einen positiven Test (also in unserem Beispiel eine erste Messung über 140 mmHg), gehen wir auch bei der zweiten Abzweigung den oberen Pfad in Richtung $T^+$ . Aus der Vierfeldertafel entnehmen wir die absoluten Häufigkeiten: Von den 270 hypertonen Patient:innen haben 250 Patient:innen auch ein positives Testergebnis. Die zugehörige Wahrscheinlichkeit $P(T^+|D^+)=93 \%$ ist diesmal die bedingte Wahrscheinlichkeit, dass eine bereits an Hypertonie erkrankte Person auch durch die erste Messung als hyperton eingestuft wird.

Am Ende jedes Pfads sind die aufgeführt, also die Wahrscheinlichkeit für den ganzen Pfad, in diesem Fall die Wahrscheinlichkeit für ein richtig positives Testergebnis. Diese ergeben sich aus den Werten im Innern der diagnostischen Vierfeldertafel im Verhältnis zu $n=1000$ . Die obere Wahrscheinlichkeit 25 % (250 von 1000) beschreibt z. B. die Wahrscheinlichkeit, dass eine Person an Hypertonie erkrankt ist und auch ein erstes Messergebnis größer als 140 mmHg (entspricht einem positiven Test) aufweist – die Reihenfolge der Ereignisse „Erkrankung“ und „Testergebnis“ ist dabei irrelevant (im Vergleich zu bedingten Wahrscheinlichkeit, wo das eine Ereignis dem anderen vorausgeht.) Die gemeinsame Wahrscheinlichkeit lässt sich auch aus dem Produkt der einzelnen Wahrscheinlichkeiten entlang des Pfads berechnen.

Sensitivität und Spezifität sind im Baumdiagramm in Abb. 2 auf der zweiten Stufe am obersten und untersten Pfad zu finden und gelb markiert.

Zusatzwissen

Ab und zu sind auch die Gegenwahrscheinlichkeiten von Sensitivität und Spezifität von Interesse, welche die Wahrscheinlichkeiten für falsche Testergebnisse genauer betrachten.

$P(T^-|D^+)=1-P(T^+|D^+)=1-\text{Sensitivität}=\frac{c}{a+c}$ beschreibt die Wahrscheinlichkeit, dass eine erkrankte Person als erkrankt übersehen wird und einen falsch negativen Test aufweist. In unserem Beispiel ergibt sich $P(T^-|D^+)=1-P(T^+|D^+)=1-0,93=0,07$ . Das heißt, mit einer Wahrscheinlichkeit von 7 % wird eine an Hypertonie erkrankte Person fälschlicherweise als gesund eingestuft.

Die Wahrscheinlichkeit, dass eine gesunde Person ein falsch positives Testergebnis erhält, wird durch $P(T^+|D^-)=1-P(T^-|D^-)=\frac{b}{b+d}$ berechnet. Für unser Beispiel ermitteln wir $P(T^+|D^-)=1-P(T^-|D^-)=1-0,81=0,19$ . Es besteht also mit einer Wahrscheinlichkeit von 19 % das Risiko, dass eine gesunde Person eine erste Messung aufweist, die größer als 140 mmHg ist.
Die Gegenwahrscheinlichkeiten sind somit also möglichst klein zu halten. Kannst du die Gegenwahrscheinlichkeiten auch im obenstehenden Baumdiagramm finden?

Sicht der Ärzt:innen/Patient:innen

Betrachten wir nun als nächstes die Sicht der Ärzt:innen und der Patient:innen. Wir blicken jetzt genau aus der anderen Richtung auf den Test, da wir in der Praxis nicht wissen, ob die Person tatsächlich erkrankt oder gesund ist und nur das Testergebnis vorliegen haben. D. h. der wahre Zustand ist unbekannt und nur das Testergebnis ist bekannt. Die erste Frage, die sich stellt, ist also: „Wenn das vorliegende Testergebnis positiv ist, wie hoch ist die Wahrscheinlichkeit, dass der/die Patient:in auch tatsächlich erkrankt ist?“ Diese Frage wird in einer Studie durch den positiv prädiktiven Wert (PPW) geklärt, der sich wie folgt berechnen lässt:

$P(D^+|T^+)=\frac{a}{a+b}.$

Es wird also der Anteil an Erkrankten an den insgesamt positiv getesteten Patient:innen betrachtet.

Der negativ prädiktive Wert (NPW) erklärt die zweite Frage: „Wenn das vorliegende Testergebnis negativ ist, wie hoch ist die Wahrscheinlichkeit, dass die Person auch tatsächlich gesund ist?“ und wird durch

$P(D^-|T^-)=\frac{d}{c+d}$

berechnet.

Beispiel "Blutdrucksenker"

Schauen wir uns mithilfe der bereits bekannten Vierfeldertafel (Tab. 4) die prädiktiven Werte für unser Beispiel an:

Tab. 4:
	Hyperton $D^+$	Normoton $D^-$	Gesamt
1. Messung $>=$ 140 mmHg $T^+$	$a=250$	$b=140$	$a+b=390$
1. Messung $<$ 140 mmHg $T^-$	$c=20$	$d=590$	$c+d=610$
Gesamt	$a+c=270$	$b+d=730$	$n=1000$

Wir berechnen:

PPW: $P(D^+|T^+)=\frac{a}{a+b}=\frac{250}{250+140}\approx 0,64$
NPW: $P(D^-|T^-)=\frac{d}{c+d}=\frac{590}{20+590}\approx 0,97$

Wenn die erste Blutdruckmessung einen systolischen Wert über 140 mmHg ergibt, bedeutet das also, dass nur in 64 % (PPW) der Fälle tatsächlich eine Hypertonie des/der untersuchten Patient:in vorliegt. Somit erkennt ihr nun bestimmt die Notwendigkeit von wiederholten Messungen, oder?

Weist die erste Messung hingegen einen Wert unter 140 mmHg auf, spricht dies mit einer hohen Wahrscheinlichkeit von 97 % (NPW) dafür, dass die Person tatsächlich auch gesund ist und nicht unter Bluthochdruck leidet – es ist also keine weitere Messung nötig.

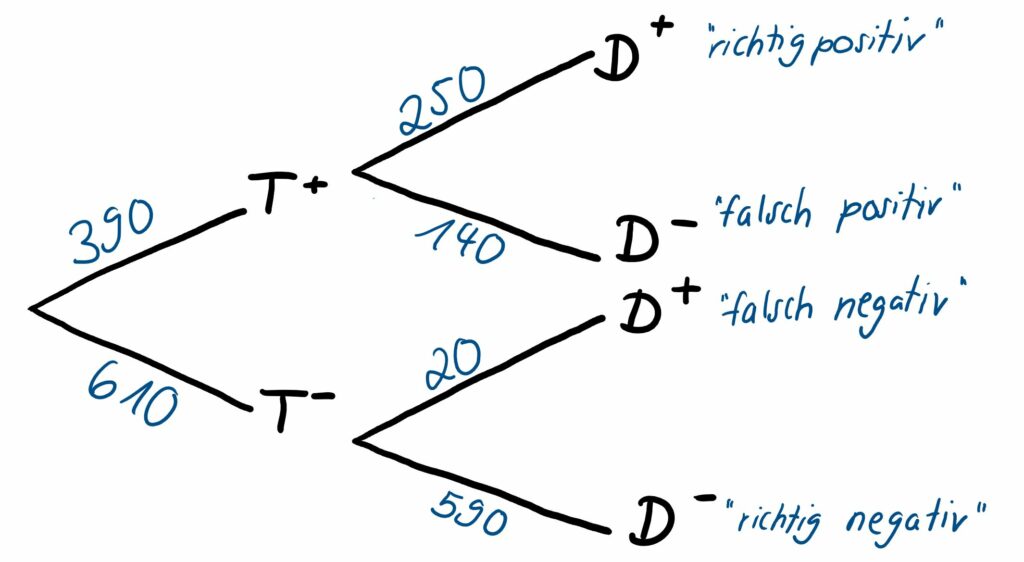
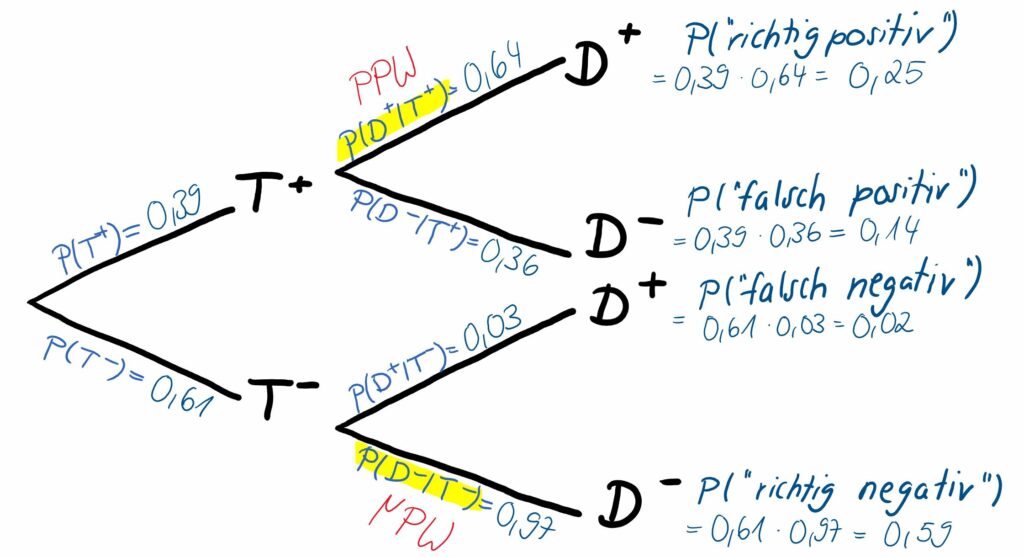
Wir wollen auch in diesem Fall die zugehörigen Baumdiagramme einmal mit absoluten Werten (Abb. 3) und einmal mit Wahrscheinlichkeiten (Abb. 4) betrachten und stellen fest, dass „nur“ die beiden Stufen, also die Reihenfolge der zwei betrachteten Ereignisse umgedreht wurde. Es wird auf der ersten Stufe das Testergebnis, also das Ergebnis der ersten Blutdruckmessung (sichtbar in den Zeilen der Vierfeldertafel), betrachtet und dann auf Stufe zwei des Baumdiagramms der wahre Krankheitszustand der Patient:innen.

Auch hier sind in Abb. 4 der PPW und der NPW wieder durch die gelb markierten bedingten Wahrscheinlichkeiten hervorgehoben, die sich in der zweiten Stufe des Baumdiagramms am oberen Pfad und am unteren Pfad befinden.

Zusammenhang der Kenngrößen und Satz von Bayes

Die zwei Versionen der Baumdiagramme und die Kenngrößen Prävalenz, Sensitivität, Spezifizität und die prädiktiven Werte hängen eng miteinander zusammen. Mithilfe des sogenannten Satz von Bayes lässt sich jede Größe auf Basis der anderen Größen ermitteln.

Beispielsweise lässt sich der PPW berechnen durch

$P(D^+|T^+)=\frac{P(D^+)\cdot P(T^+|D^+)}{[P(D^+)\cdot P(T^+|D^+)]+[P(D^-)\cdot P(T^+|D^-)]}$

Lasst euch durch die komplizierte Schreibweise der Formel nicht abschrecken – wenn man sie ausschreibt, sieht sie schon deutlich verständlicher aus:

$PPW=\frac{\text{Prävalenz}\cdot\text{Sensitivität}}{\text{Prävalenz}\cdot\text{Sensitivität}+(1-\text{Prävalenz})\cdot(1-\text{Spezifität})}$

und analog

$NPW=\frac{(1-\text{Prävalenz})\cdot\text{Spezifität}}{(1-\text{Prävalenz})\cdot\text{Spezifität}+Prävalenz\cdot(1-\text{Sensitivität})}$

In Kurzform wird der Satz von Bayes also genutzt, um eine bedingte Wahrscheinlichkeit zu berechnen, wenn die „umgekehrte“ bedingte Wahrscheinlichkeit bereits bekannt ist. Die genaue Herleitung der Formel und die Erklärung über den Zusammenhang der Baumdiagramme könnt ihr in der untenstehenden Box nachlesen.

Betrachtet man den Zusammenhang der Kenngrößen genauer, kann man überlegen, wie sich die prädiktiven Werte verändern, wenn sich jeweils Prävalenz, Sensitivität und Spezifität verändern (unter der Annahme, dass die jeweils anderen Werte konstant bleiben). Die Ergebnisse sind in der folgenden Tabelle zusammengefasst:

Änderung	Auswirkung PPW	Auswirkung NPW
Prävalenz steigt	▲ steigt	▼ sinkt
Sensitivität steigt	▲ steigt	▲ steigt
Spezifität steigt	▲ steigt	▲ steigt

Die Änderung der Prävalenz sorgt dabei für besonders starke Veränderungen. Besonders kritisch wird es, wenn ein diagnostischer Test bei seltenen Erkrankungen oder niedrigen Prävalenzen genutzt wird: der PPW ist dann sehr niedrig, was bedeutet, dass es bei einem Einsatz des Tests zu vielen Fehldiagnosen im Sinne falsch positiver Ergebnisse käme und teils mit großen psychischen Belastungen, unnötiger weiterer Diagnostik oder sogar unnötigen Behandlungen für die Patient:innen einhergeht. Lasst euch also als zukünftige Ärzt:innen nicht täuschen: Nur, weil eine erkrankte Person mit einer Wahrscheinlichkeit von 99 % auch ein positives Testergebnis erhält, gilt nicht, dass ihr euch bei einem positiven Testergebnis zu 99 % sicher sein könnt! Die Wahrscheinlichkeit, dass ein positives Testergebnis richtig ist und tatsächlich auf eine Erkrankung hinweist, kann bei sehr seltenen Erkrankungen (geringe Prävalenz) deutlich niedriger sein.

Zusatzwissen

Herleitung Satz von Bayes

Um zu erklären, wie sich der Satz von Bayes ergibt, wollen wir uns im ersten Schritt nochmal genauer den Zusammenhang zwischen den Baumdiagrammen aus Testentwickler:innen-Sicht und aus Ärzt:innen/Patient:innen-Sicht anschauen.

Dazu versuchen wir das Baumdiagramm aus Ärzt:innen/Patient:innen-Sicht aus dem Baumdiagramm aus Testentwickler:innen-Sicht herzuleiten:

Erstmals fällt uns auf, dass die gleichen gemeinsamen Wahrscheinlichkeiten der Pfade insgesamt betrachtet werden (ganz rechts, nur in der Reihenfolge vertauscht), sodass wir diese einfach übernehmen können.
Als nächstes wollen wir die einfachen Wahrscheinlichkeiten $P(T^+)$ und $P(T^-)$ ermitteln.Das können wir mithilfe der gemeinsamen Wahrscheinlichkeiten: Die Wahrscheinlichkeit, dass eine Person einen positiven Test erhält, ist die Summe der Wahrscheinlichkeit, dass eine erkrankte Person einen positiven Test erhält und der Wahrscheinlichkeit, dass eine gesunde Person einen positiven Test erhält. Also $P(T^+)=P(\text{„richtig positiv“})+P(\text{„falsch positiv“})$ . Die Berechnung von $P(T^-)$ erfolgt analog. Diese Regel wird auch als Summenregel bezeichnet, da die gemeinsamen Wahrscheinlichkeiten zweier Pfade aufsummiert werden.
Im letzten Schritt berechnen wir die bedingten Wahrscheinlichkeiten, inklusive der gelb markierten prädiktiven Werte. Wir wissen schon, dass sich die gemeinsamen Wahrscheinlichen am Ende der Pfade durch Multiplizieren der einzelnen Wahrscheinlichkeiten des Pfades ergeben. Diese Eigenschaft bezeichnen wir nun als Produktregel, also $P(\text{„richtig positiv“})=P(T^+)\cdot P(D^+|T^+)$ . Wir können die Formel umstellen zu $P(D^+|T^+)=\frac{P(\text{„richtig positiv“})}{P(T^+)}$ .

Nach Durchführung dieser drei Schritte haben wir das Baumdiagramm ermittelt. Aus der letzten Formel in Schritt 3 ergibt sich nun durch weiteres Umstellen mithilfe der gelernten Regeln der berühmte Satz von Bayes:

P(D^+|T^+)

=\frac{P(\text{„richtig positiv“})}{P(T^+)}

Umkehrung Produktregel

=\frac{P(D^+)\cdot P(T^+|D^+)}{P(\text{„richtig positiv“})+P(\text{„falsch positiv“})}

Zähler: Produktregel, Nenner: Summenregel

=\frac{P(D^+)\cdot P(T^+|D^+)}{[P(D^+)\cdot P(T^+|D^+)]+[P(D^-)\cdot P(T^+|D^-)]}

Nenner: jeweils Produktregel

PPW

=\frac{\text{Prävalenz}\cdot\text{Sensitivität}}{\text{Prävalenz}\cdot\text{Sensitivität}+(1-\text{Prävalenz})\cdot(1-\text{Spezifität})}

ausgeschrieben

Eine Einführung zum Satz von Bayes findest du in Kapitel 6.2.6 in Weiß 2013.

Zusatzwissen

Wie wird die Güte eines diagnostischen Tests bewertet?

Am besten wäre es natürlich, wie man auch in der obigen Tabelle sieht, wenn sowohl Sensitivität als auch Spezifität einen möglichst hohen Wert annehmen. In der Praxis ist allerdings häufig ein Parameter höher und der andere niedriger. Wenn man einen Trenn- bzw. Grenzwert festlegen kann, kann man einen Kompromiss zwischen Sensitivität und Spezifität eingehen. Dafür muss entschieden werden, welcher Wert eine wichtigere Rolle für den aktuellen Fall spielt. Geht es zum Beispiel darum, eine Krankheit zu diagnostizieren, die unentdeckt meist tödlich verläuft aber entdeckt gut heilbar ist, wäre es fatal viele Erkrankte durch ein negatives Testergebnis zu „übersehen“. Es sollte also auf eine hohe Sensitivität Wert gelegt werden, auch wenn damit das Risiko für mehr falsch positive Testergebnisse und damit psychischem Stress für falsch diagnostizierte Patient:innen steigt. In der Praxis wird aus diesem Grund bei positivem Testergebnis häufig ein zweiter, anderer Bestätigungstest durchgeführt, wie z. B. im Kontext der HIV-Testung, wo bei positivem ELISA-Test eine Bestätigung durch die Western Blot-Methode angehängt wird. Voraussetzung ist dabei wiederum, dass es ein guter Test zur Bestätigung existiert.

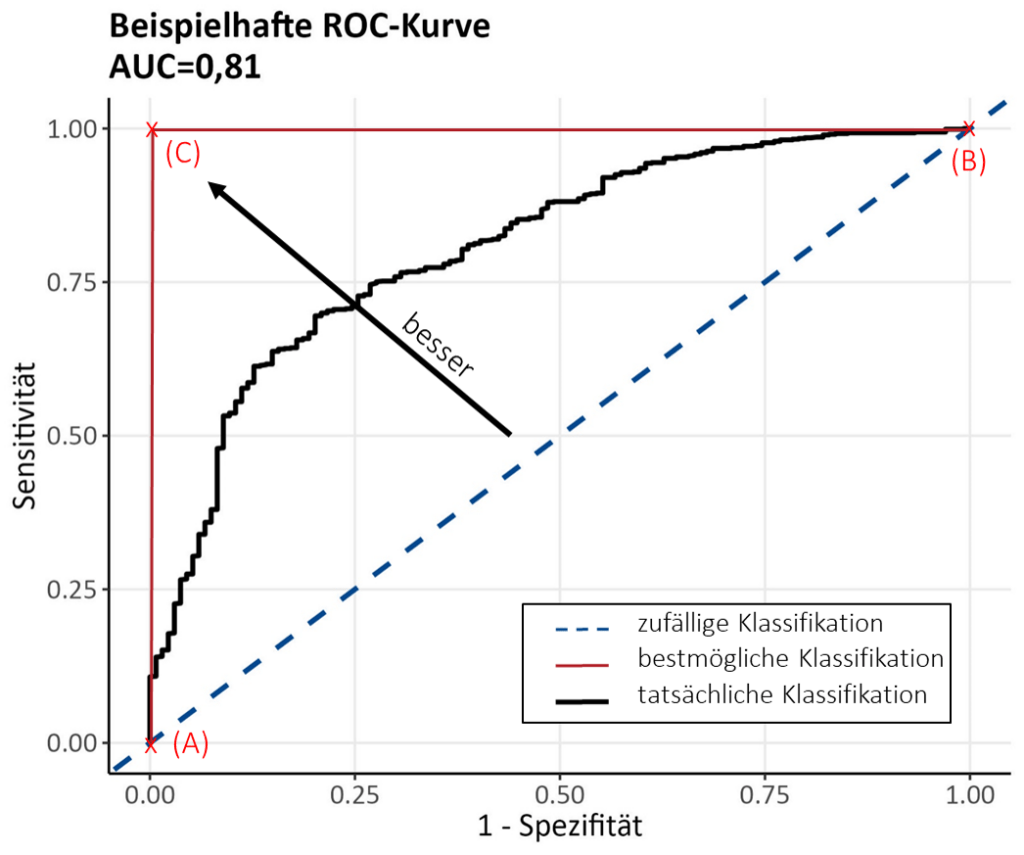
Den Kompromiss zwischen den zwei Kenngrößen wollen wir genauer anhand der sogenannten Receiver Operating Characteristic Curve (ROC-Kurve, Abb. 5) betrachten. Sie stellt den Kompromiss grafisch dar und gibt einen Anhaltspunkt dafür, welcher Grenzwert in Bezug auf einen geeigneten Trade-Off zwischen Sensitivität und Spezifität gewählt werden sollte.

Wir sehen auf der y-Achse die Sensitivität und auf der x-Achse die Gegenwahrscheinlichkeit der Spezifität, also $1-\text{Spezifität}$ . In der Grafik ist abgebildet, welche Werte Sensitivität und Spezifität für unterschiedliche Grenzwerte annehmen. Für jeden möglichen Grenzwert berechnen wir also Sensitivität und Spezifität und zeichnen den entsprechenden Punkt in der Grafik ein, sodass letztendlich die Kurve entsteht.

Für ein besseres Verständnis der Kurve wollen wir uns nun die zwei Extrempunkte der Grafik (A) und (B) anschauen: Der Punkt ganz links unten (A) wird damit erreicht, wenn alle Patient:innen, egal ob gesund oder erkrankt, ein negatives Testergebnis erhalten würden. Logischerweise bekommen damit dann auch 100 % der gesunden Patient:innen ein richtig negatives Ergebnis und die Spezifität liegt bei 100 %. Da die x-Achse allerdings 1-Spezifität abbildet, findet sich ein Wert von 0 wieder. Die Sensitivität hingegen liegt bei 0 %, da keine einzige erkrankte Person einen positiven Test aufweist. Je eher („schneller“) der Test positiv ausfällt (dies ist eben abhängig vom gewählten Grenzwert), desto weiter nach rechts bewegen wir uns auf der Kurve.

Das andere Extrem, nämlich, dass alle Patient:innen ein positives Testergebnis erhalten, wird in Punkt (B) abgebildet. Analog zur Erklärung zu Punkt (A) haben wir an diesem Punkt eine Sensitivität von 100 %, allerdings eine Spezifität von 0 % (in der Grafik

1-\text{Spezifität}=100\%

). Die Frage ist nun welcher Grenzwert in Bezug auf die Gesamt-Diagnosegüte am besten geeignet ist. Eine Maßzahl zur Gesamtgüte eines Tests ist die Area Under the Curve (AUC), also die Fläche unter der Kurve. Theoretisch gesehen wäre, wie bereits erläutert, eine Spezifität und Sensitivität von 100 % das bestmögliche Ergebnis. Dieser Punkt würde in Punkt (C) ganz oben links erreicht werden und die Fläche unter der Kurve läge bei

100\%\cdot 100\% = 1

. Wie man anhand der eingezeichneten Kurve allerdings erkennen kann, wird dieser Punkt in der Praxis meist nicht erreicht. Je weiter die tatsächliche Kurve von der optimalen Kurve weg liegt und folglich je kleiner die Fläche unter der Kurve (die AUC) wird, desto schlechter ist der Test insgesamt. Das schlechtmöglichste Ergebnis wäre die Diagonale von (A) zu (B), bei der jedes Mal rein zufällig (also mit einer Wahrscheinlichkeit von 50 %) entschieden würde, ob eine Person erkrankt oder gesund ist. Das Ergebnis der AUC läge dann bei 0,5. Das Ziel ist somit, einen Test mit großer AUC zu entwickeln und dann den Grenzwert so zu wählen, dass wir uns auf der ROC-Kurve möglichst weit oben links in der Ecke befinden. Man sieht, dass in diesem oberen linken Bereich, viele Grenzwerte ähnliche Ergebnisse der Sensitivität und Spezifität liefern. Dann kann je nach Anwendungsfall entschieden werden, welcher Wert (Sensitivität vs. Spezifität) eine größere Bedeutung einnehmen sollte und der Grenzwert aus dem sinnvollen Bereich so gewählt werden, dass der relevantere Wert im Fokus liegt. Eine Kenngröße, die zu Rate gezogen werden kann, um einen geeigneten Grenzwert zu bestimmen, ist der sogenannte Youden-Index. Er wird wie folgt berechnet:

\text{Youden-Index}=\text{Sensitivität in \%}+\text{Spezifizität in \%}-100

. Allerdings beachtet dieser eben nicht den Fall, dass eine Kenngröße eine größere Relevanz im Anwendungsfall einnehmen kann, sondern bewertet Sensitivität und Spezifität als gleich wichtig.

LITERATURVERZEICHNIS

Die Inhalte dieser Seite sind angelehnt an:

Weiß, Christel (2013): Studien zu Diagnostik und Prävention. In: Christel Weiß (Hg.): Basiswissen Medizinische Statistik. Mit 20 Tabellen. 6., überarbeitete Auflage. Berlin, Heidelberg: Springer (Springer Lehrbuch), S. 259–273, Kapitel 14.1.

Fußnoten

1
Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2023), Universitätsklinikum Hamburg-Eppendorf.
2
Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2023), Universitätsklinikum Hamburg-Eppendorf.
3
Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2023), Universitätsklinikum Hamburg-Eppendorf.
4
Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2023), Universitätsklinikum Hamburg-Eppendorf.
5
eigene Darstellung, Daten simuliert nach Christian Fang (2022): ROC curve and AUC from scratch using simulated data in R and Python. Online verfügbar unter https://christianfang95.github.io/posts/2022/09/roc-auc/, zuletzt aktualisiert am 21.03.2023, zuletzt geprüft am 22.03.2023.