Confounding, Bias & Co.
Studienauswertung
Die Inferenzstatistik verläuft in der Praxis nicht ohne Fehler bzw. Irrtümer, weshalb in diesem Abschnitt typische Probleme wie fehlende Werte, Confounding und Bias thematisiert werden sollen.
Einerseits kann es passieren, dass bei der Interpretation der vorliegenden Ergebnisse Fehler entstehen. Ein häufiger Fehler ist es z. B., dass der/die Anwender:in eine beobachtete Korrelation zwischen zwei Größen mit Kausalität verwechselt (Korrelation ≠ Kausalität). Durch einen großen Korrelationskoeffizienten wird lediglich beschrieben, dass die beiden Variablen gemeinsam variieren. Ob eine der beiden Variablen dabei die andere direkt beeinflusst, was man für Aussagen über die Kausalität untersucht, bleibt offen. Die Korrelation schaut sich also nur die gemeinsame Variation zwischen Variablen an, die Kausalität geht einen Schritt weiter und betrachtet Ursache-Wirkungs-Beziehungen. Schlüsse über eine zugrundeliegende Kausalität müssen zusätzlich durch inhaltliche Überlegungen, wie eine Einsicht in Gesetzmäßigkeiten oder nachweisbare Nachzeitigkeit, legitimiert werden.
Andererseits können Fehler bereits beim Design der Studie/des statistischen Tests oder bei dessen Durchführung auftreten. Es wird z. B. zwischen Confounding und Bias unterschieden.
Confounding
Confounding tritt auf, wenn sowohl das betrachtete Outcome als auch die Exposition durch eine dritte Variable beeinflusst werden. Diese Störvariable wird dann als Confounder bezeichnet. Die Konsequenz bei Nicht-Berücksichtigung ist, dass eine Korrelation zwischen Exposition und Outcome vorliegt, die jedoch keinen kausalen Zusammenhang darstellt. Man spricht auch von einer Scheinkorrelation. Eine Lösung für dieses Problem ist es, bereits vor Beginn der Analyse Überlegungen über mögliche Confounder anzustellen und diese dann in der statistischen Analyse zu berücksichtigen (z. B. durch Stratifizierung oder als zusätzliche Kovariablen in einer multiplen linearen Regression).
Beispiel "Blutdrucksenker"
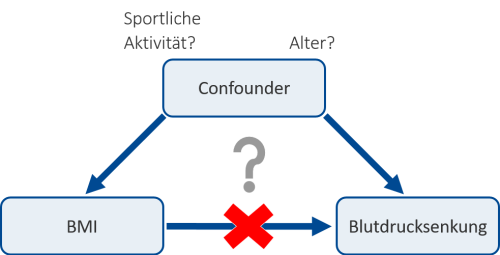
In unserem Beispiel (siehe Abb. 1) wurde der lineare Zusammenhang zwischen BMI und der Blutdrucksenkung untersucht und eine negative Korrelation gefunden. Dies bedeutet nicht zwangsläufig, dass ein höherer BMI tatsächlich auch die Ursache für eine geringere Blutdrucksenkung ist (keine kausale Ursache-Wirkung-Beziehung). Beispielsweise hätte es sein können, dass die Variablen Alter oder sportliche Aktivität sowohl einen Einfluss auf den BMI als auch auf das Outcome Blutdrucksenkung ausüben und damit Confounder in der Analyse darstellen. Deshalb ist es sinnvoll, auch diese Variablen zu erheben und in der Analyse (wie im multiplen linearen Regressionsmodell) zu berücksichtigen.
Bias
Von Bias spricht man bei systematischen Fehlern und Verzerrungen. Ein Selektionsbias tritt auf, wenn die Stichprobe nicht repräsentativ für die Grundgesamtheit ist. Dies ist häufig der Fall, wenn die Teilnahmebereitschaft an Studien niedrig ist und bestimmte Bevölkerungsgruppen nicht in die Studie eingeschlossen werden können oder frühzeitig aus der Studie austreten (Loss to Follow-up oder Drop-Outs).
Eine andere Art der Verzerrung ist der sogenannte Informationsbias, der systematische Fehler bei der Datenerhebung bezeichnet. Diese Fehler können z. B. durch unvollständig oder falsch ausgefüllte Fragebögen, fehlerhafte Messgeräte oder bei Fehlern in der Datenübertragung eintreten. Eine spezifische Form des Informationsbias ist der Recall Bias, der bei retrospektiven Studien auftritt, wenn sich die Versuchspersonen nicht mehr realitätsgetreu an abgefragte Gegebenheiten (z. B. Symptome) erinnern können.
Auch durch Zufall können in der Praxis Fehler auftreten. Man spricht dann von einem Zufallsfehler.
Zusatzwissen
Umgang mit fehlenden Werten
Als fehlende Werte (oder auch Missing Values bzw. Missings) werden Lücken in den Daten bezeichnet, also wenn z. B. für eine Versuchsperson und eine spezifische Variable kein Datenpunkt vorliegt. Es kann verschiedene Ursachen haben, warum Werte im Datensatz fehlen: Sie können zufällig fehlen, wenn es z. B. (technische) Probleme bei der Datenübertragung gab oder die interviewende Person aus Versehen eine Frage übersprungen hat. Komplizierter wird es, wenn die Daten aus systematischen Gründen fehlen, z. B. weil eine Person keine Antwort geben möchte, weil die Antwort selbst ihr unangenehm ist. Wird dieses systematische Fehlen von Daten ignoriert, kann dies zu Verzerrungen und Ungenauigkeiten in den Schätzergebnissen der statistischen Methoden führen.
Für den Umgang mit fehlenden Werten kommen verschiedene Methoden in Frage:
Stellt man fest, dass eine Versuchsperson bei sehr vielen Variablen Lücken (Lücken in einer Zeile des Datensatzes) aufweist oder dass eine bestimmte Variable nur von sehr wenigen Versuchspersonen erhoben werden konnte (Lücken in einer Spalte des Datensatzes), ist es manchmal sinnvoll, die gesamte Zeile oder Spalte aus der Datenanalyse auszuschließen. Diese Methode hat allerdings zwei große Nachteile: Erstens führt sie bei nicht-zufällig fehlenden Daten zu Verzerrungen und zweitens wird der Datensatz verkleinert und teilweise gehen auch nützliche Daten verloren.
Eine Möglichkeit mit fehlenden Werten umzugehen, ist die sogenannte Imputation. Bei der Imputation wird ein „neuer“ Wert in die vorhandene Datenlücke eingesetzt. Aber wie kommt dieser Wert zustande? Dazu gibt es verschiedene Ansätze: Bei metrischen Variablen kann der Mittelwert der vorhandenen Daten der jeweiligen Variablen eingesetzt werden. Fehlt z. B. bei einer Versuchsperson die Variable „Körpergröße“ würde in unserem Beispiel der Wert 175,8 eingesetzt werden. Auch der Median oder Modalwert kommen je nach Skalenniveau der Variable als fixe Imputationswerte in Frage.
Eine komplexere Methode ist es, den fehlenden Wert als Funktion der vorhandenen Werte anderer Variablen des Datensatzes zu schätzen. Dies kann z. B. mithilfe eines linearen Regressionsmodells erfolgen. Wir werden an dieser Stelle nicht weiter auf diese Methode eingehen, lest aber gerne in diesem Beitrag von der FU Berlin mehr dazu nach, falls es euch interessiert.
Es gibt außerdem statistische Analysemethoden, die auch auf einen Datensatz mit fehlenden Werten angewendet werden können, aber hier nicht weiter thematisiert werden sollen.
Fazit
In der Praxis ist es nicht möglich, alle Fehler gänzlich zu vermeiden. Deshalb ist es wichtig, mögliche Fehlerquellen zu kennen, um so von vornherein wenigstens einigen Fehlern, wie z. B. Confounding und Bias, aus dem Weg gehen zu können und ein Bewusstsein für mehr Vorsicht bei der Interpretation der Ergebnisse zu entwickeln.
LITERATURVERZEICHNIS
Die Inhalte dieser Seite sind angelehnt an:
Fußnoten
- 1Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2023), Universitätsklinikum Hamburg-Eppendorf.