Korrelation in SPSS
Korrelationen werden betrachtet, um den Zusammenhang zwischen Variablen feststellen zu können. Im EpiBioManual wurde bereits der Pearson-Korrelationskoeffizient händisch berechnet und erläutert. Wir wollen uns nun ansehen, wie wir diesen in SPSS berechnen können. Außerdem werden wir den Zusammenhang zwischen zwei Variablen mithilfe eines Streudiagramms visualisieren.
Beispiel "Blutdrucksenker"
Es soll untersucht werden, ob es einen Zusammenhang zwischen dem BMI der Patient:innen und der Senkung ihres Blutdrucks nach 5 Wochen gibt. Dazu wird der Pearson-Korrelationskoeffizient und ein Streudiagramm für die metrischen Varialen BMI und BD_senk betrachtet.
voraussetzungen
… für den Pearson-Korrelationskoeffizienten:
Umsetzung in SPSS
Im SPSS-Menü: Analysieren » Korrelation » Bivariat …
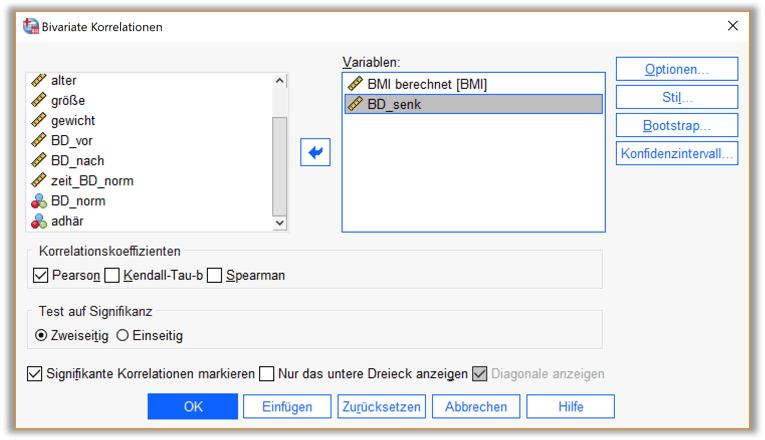
Im Dialogfenster (vgl. Abb. 1) werden die Variablen angegeben, für die die Korrelation berechnet werden soll. Wir wählen aus der Liste die Variablen BD_senk und BMI aus und übertragen sie mithilfe des Pfeil-Symbols in das ‚Variablen‘-Feld. Hier ist es auch möglich, mehr als zwei Variablen zu betrachten, für die dann jeweils bivariate Korrelationen untereinander in einer Tabelle ausgegeben werden.
Zusätzlich müssen die Häkchen bei den Korrelationskoeffizienten gesetzt werden, die uns interessieren. In unserem Fall also das Häkchen bei ‚Pearson‘. Auf die Alternativen – den Spearman– und den Kendall-Tau-b–Korrelationskoeffizienten – wird im Rahmen des EpiBioManuals nicht weiter eingegangen.
Syntax
DATASET ACTIVATE DataSet1.
CORRELATIONS
/VARIABLES=BMI BD_senk
/PRINT=TWOTAIL NOSIG FULL
/MISSING=PAIRWISE.
Interpretation des SPSS-Outputs
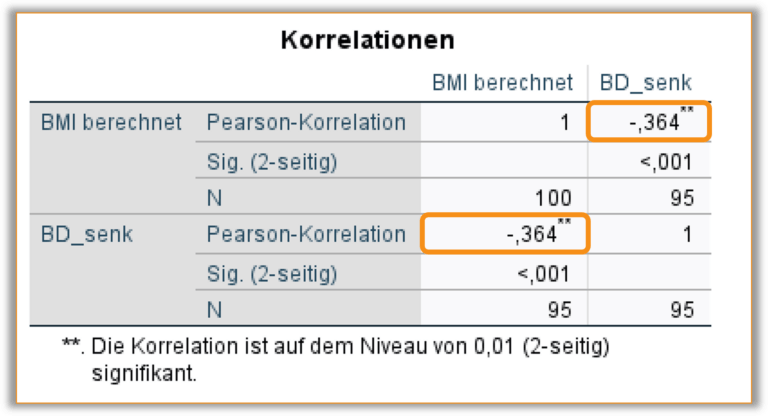
Die Tabelle in Abb. 2 zeigt das Ergebnis der Korrelationsberechnung. Es wird schnell ersichtlich, dass die Tabelle symmetrisch um die Diagonale herum aufgebaut ist.
Hier kann man den Korrelationskoeffizienten jeweils in einem der Felder ablesen, die beide Variablen BD_senk und BMI beinhalten. Das heißt, der Pearson-Korrelationskoeffizient ist, wie in unseren manuellen Berechnungen, r_{xy}= -0,364. Die andere Diagonale zeigt jeweils 1 an, da die Korrelation einer Variablen mit sich selbst immer 1 ergibt.
Wie im EpiBioManual genauer erklärt, handelt es sich um eine moderate negative Korrelation zwischen dem BMI und der Senkung des systolischen Blutdrucks.
Umsetzung in SPSS
Im SPSS-Menü: Grafik » Streu-/Punktdiagramm …
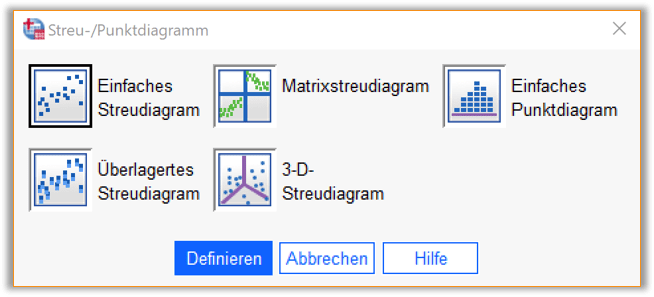
Im Dialogfenster (vgl. Abb. 3) wird zunächst ‚Einfaches Streudiagramm‘ ausgewählt.
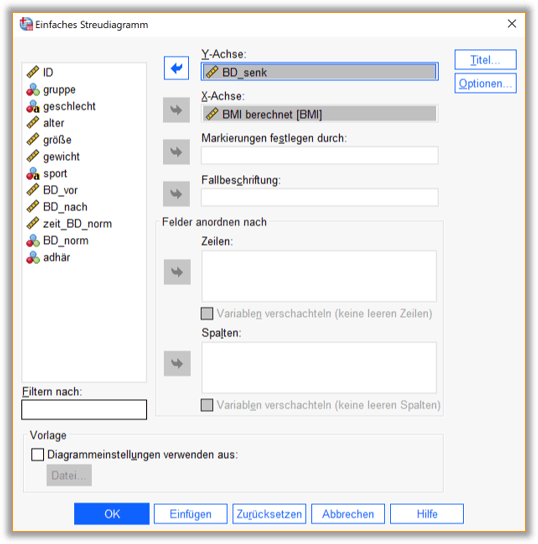
Nach dem Klick auf ‚Definieren‘ werden im nächsten Dialogfenster (vgl. Abb. 4) die Variablen angegeben, für die das Streudiagramm erstellt werden soll: Wir wählen die Variable BMI für die X-Achse unseres Diagramms und die Variable BD_senk für die Y-Achse aus.
Syntax
DATASET ACTIVATE DataSet1.
GRAPH
/SCATTERPLOT(BIVAR)=BMI WITH BD_senk
/MISSING=LISTWISE.
Interpretation des SPSS-Outputs
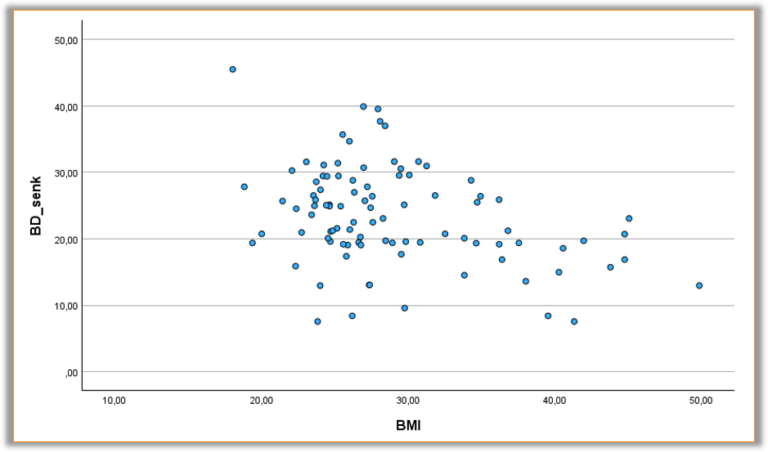
Das Streudiagramm in Abb. 5 mit dem BMI auf der X-Achse und der Blutdrucksenkung auf der Y-Achse hilft, den Zusammenhang der Variablen grafisch nachzuvollziehen.
Hier lässt sich auch wieder der moderat negative Zusammenhang zwischen den Variablen erkennen.
Fußnoten
- 1Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2025), Universitätsklinikum Hamburg-Eppendorf.
- 2Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2025), Universitätsklinikum Hamburg-Eppendorf.
- 3Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2025), Universitätsklinikum Hamburg-Eppendorf.
- 4Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2025), Universitätsklinikum Hamburg-Eppendorf.
- 5Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2025), Universitätsklinikum Hamburg-Eppendorf.