Lineare Regression in SPSS
Um Zusammenhänge zwischen Variablen spezifischer zu analysieren, verwendet man ein Regressionsmodell. Hier gibt es wieder je nach Anzahl der Variablen und Skalenniveaus verschiedene Regressionen. Das einfachste Modell ist eine lineare Einfach-Regression, bei der der Einfluss einer Variable (unabhängige Variable) auf eine metrische Zielgröße (abhängige Variable) erklärt wird. In einer multiplen linearen Regression wird der Einfluss mehrerer unabhängiger Variablen auf eine metrische abhängige Variable untersucht. Beide Analysen werden in SPSS auf die gleiche Art und Weise durchgeführt und deshalb auf dieser Seite gemeinsam behandelt.
Außerdem wollen wir uns anschauen, wie wir eine lineare Regressionsgerade in einem bivariaten Streudiagramm einzeichnen können.
Beispiel "Blutdrucksenker"
Es soll untersucht werden, inwiefern der BMI der Patient:innen einen Einfluss auf die Senkung ihres Blutdrucks nach 5 Wochen hat. Somit wird die metrische Variable BMI als unabhängige Variable und die metrische Variable BD_senk als abhängige Variable in der Analyse betrachtet.
voraussetzungen
- Es wird von einem linearen Zusammenhang zwischen der (bzw. den) unabhängigen Variable(n) und der abhängigen Variable ausgegangen.
- Die abhängige Variable ist metrisch skaliert und annähernd normalverteilt.
- Auf weitere Voraussetzungen, die für eine sinnvolle Interpretierbarkeit der Ergebnisse gegeben sein müssen (z. B. Homoskedastizität und Unabhängigkeit der Residuen, keine Multikollinearität) wird im Rahmen des EpiBioManuals nicht eingegangen.
Umsetzung in SPSS
Im SPSS-Menü: Analysieren » Regression » Linear …
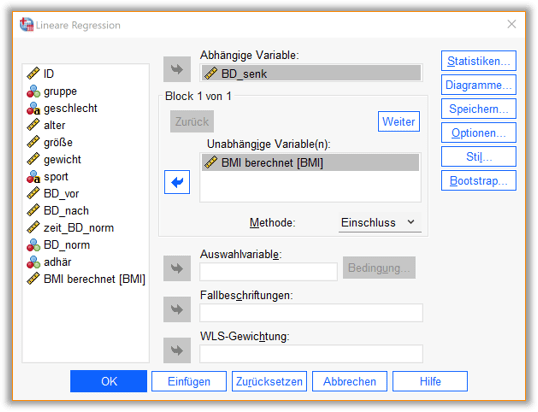
Im Dialogfenster (vgl. Abb. 1) zur Durchführung einer linearen Regression müssen zunächst die abhängige Variable und die unabhängige(n) Variable(n) spezifiziert werden. Wir fügen als abhängige Variable BD_senk ein und als unabhängige Variable den BMI. Für eine multiple lineare Regression könnten wir in das Feld unabhängige Variablen weitere Einflussvariablen einfügen. Unter ‚Statistiken…‘ könnt ihr zusätzlich auswählen, dass 95 %-Konfidenzintervalle für die geschätzten Regressionskoeffizienten ausgegeben werden sollen.
Syntax
DATASET ACTIVATE DataSet1.
REGRESSION
/MISSING LISTWISE
/STATISTICS COEFF OUTS CI(95) R ANOVA
/CRITERIA=PIN(.05) POUT(.10) TOLERANCE(.0001)
/NOORIGIN
/DEPENDENT BD_senk
/METHOD=ENTER BMI.
Interpretation des SPSS-Outputs
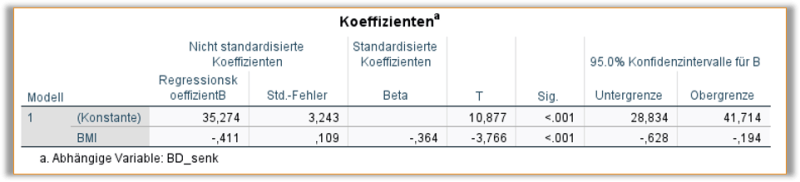
Wir erhalten den in Abb. 2 gezeigten Output zu den Koeffizienten der linearen Einfach-Regression. In einer multiplen Regression würde die Tabelle um eine zusätzliche Zeile pro Variable erweitert werden.
Zuerst betrachten wir die Regressionskoeffizienten in der zweiten Spalte der Outputtabelle. Das Vorzeichen der Regressionskoeffizienten zeigt, ob die jeweilige Variable im Mittel einen positiven, oder negativen Einfluss auf die abhängige Variable hat. Die Konstante von 35,274 ist unser \widehat{a}, also unser Achsenabschnitt. Sie gibt in diesem Falle die hypothetische Blutdrucksenkung nach 5 Wochen an, die bei einem BMI von 0 (in der Realität unmöglich) resultieren würde. Da dieser Wert nicht relevant ist, um den Zusammenhang zwischen Einfluss- und Zielgröße zu beschreiben, wird ihm in der Berichterstattung meist keine große Bedeutung beigemessen. Der Regressionskoeffizient in der Zeile der Variable BMI ergab \widehat{b}=-0,411.
Somit ergibt sich, vergleichbar mit unseren händischen Berechnungen, die folgende Regressionsgerade
\widehat{BD_{senk}}=35,274-0,411\cdot BMI.
Steigt der BMI um eine Einheit, dann sinkt die Blutdrucksenkung nach 5 Wochen im Durschnitt um 0,411 mmHg. Somit erwarten wir bei Patient:innen mit höherem BMI eine geringere Blutdrucksenkung nach 5 Wochen als bei Patient:innen mit geringerem BMI.
In der sechsten Spalte der Tabelle sind die p-Werte abgebildet, die Aussage über die Signifikanz der betrachteten Einflüsse geben (Es wird übrigens mithilfe eines t-Tests untersucht, ob der Koeffizient signifikant von 0 verschieden ist). In diesem Fall ist der Einfluss vom BMI auf die Absenkung signifikant, da der p-Wert jeweils < 0,05, was unserem gewählten Signifikanzniveau \alpha entspricht, ist.
Die siebte und achte Spalte geben die Unter- und Obergrenze des 95%-Konfidenzintervalls je Schätzer an. Da das Konfidenzintervall für den BMI mit [-0.628; -0.194] nicht die Null überdeckt, spricht dies erneut für einen signifikanten Einfluss des BMI auf die Absenkung des Blutdrucks.
In Abb. 3 sind zwei weitere Tabellen abgebildet, die im Zuge der Durchführung einer linearen Regression in SPSS ausgegeben werden. In der ‚Modellzusammenfassung‘ wird das Bestimmtheitsmaß r^2 = 0,132 angezeigt, das zur Beurteilung der Modellgüte herangezogen wird. In diesem Fall heißt es, dass lediglich 13 % der Gesamtstreuung in der Blutdrucksenkung durch den BMI erklärt werden können und wir davon ausgehen können, dass es besser geeignete Modelle zur Modellierung der Blutdrucksenkung gibt.
Außerdem sollte anhand der zweiten Tabelle ‚ANOVA‘ kontrolliert werden, ob das Modell insgesamt einen signifikanten Beitrag zur Erklärung der abhängigen Variable liefert. Insbesondere bei multiplen Regressionen ist diese Untersuchung relevant. Der sogenannte F-Test auf Gesamtsignifikanz testet die Nullhypothese, dass ausnahmslos alle Koeffizienten gleich 0 sind. Ein p-Wert < 0,05 spricht dafür, dass mindestens einer geschätzten Regressionskoeffizienten signifikant von 0 verschieden ist und somit das Modell insgesamt zur Erklärung der abhängigen Variable beiträgt.
STREUDIAGRAMM MIT REGRESSIONSGERADE
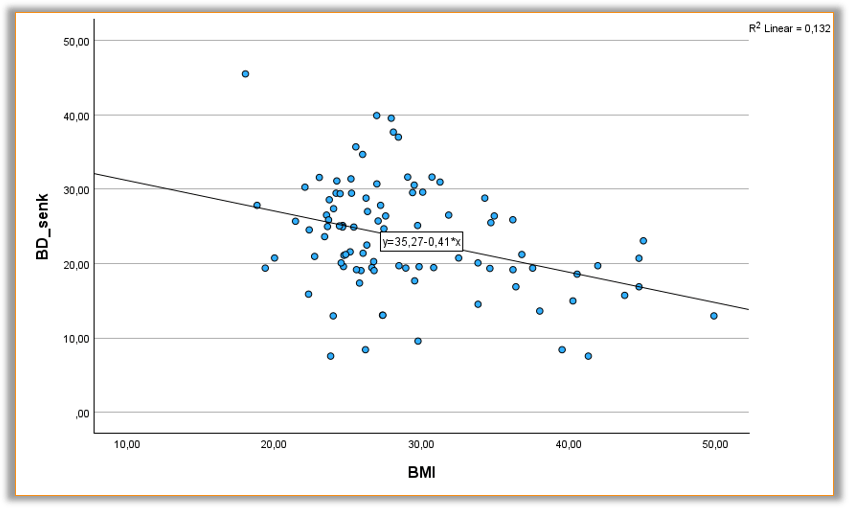
Wir haben auf der Seite Korrelation in SPSS bereits gelernt, wie man ein Streudiagramm für die Visualisierung des Zusammenhangs zwischen zwei metrischen Variablen erstellt. In dieses Streudiagramm wollen wir nun auch noch die oben berechnete Regressionsgerade einzeichnen.
Dafür erstellen wir zunächst erneut das Streudiagramm mit der unabhängigen Variable BMI auf der x-Achse und der ahängigen Variable BD_senk auf der y-Achse.
Im Ausgabefenster von SPSS öffnen wir durch einen Doppelklick auf das Streudiagramm den Diagrammeditor (vgl. Abb. 4). Darin findet sich in der Menüleiste die Option, eine Anpassungslinie einzufügen. Es öffnet sich ein weiteres Dialogfenster, in dem die lineare Anpassungslinie ausgewählt werden kann.
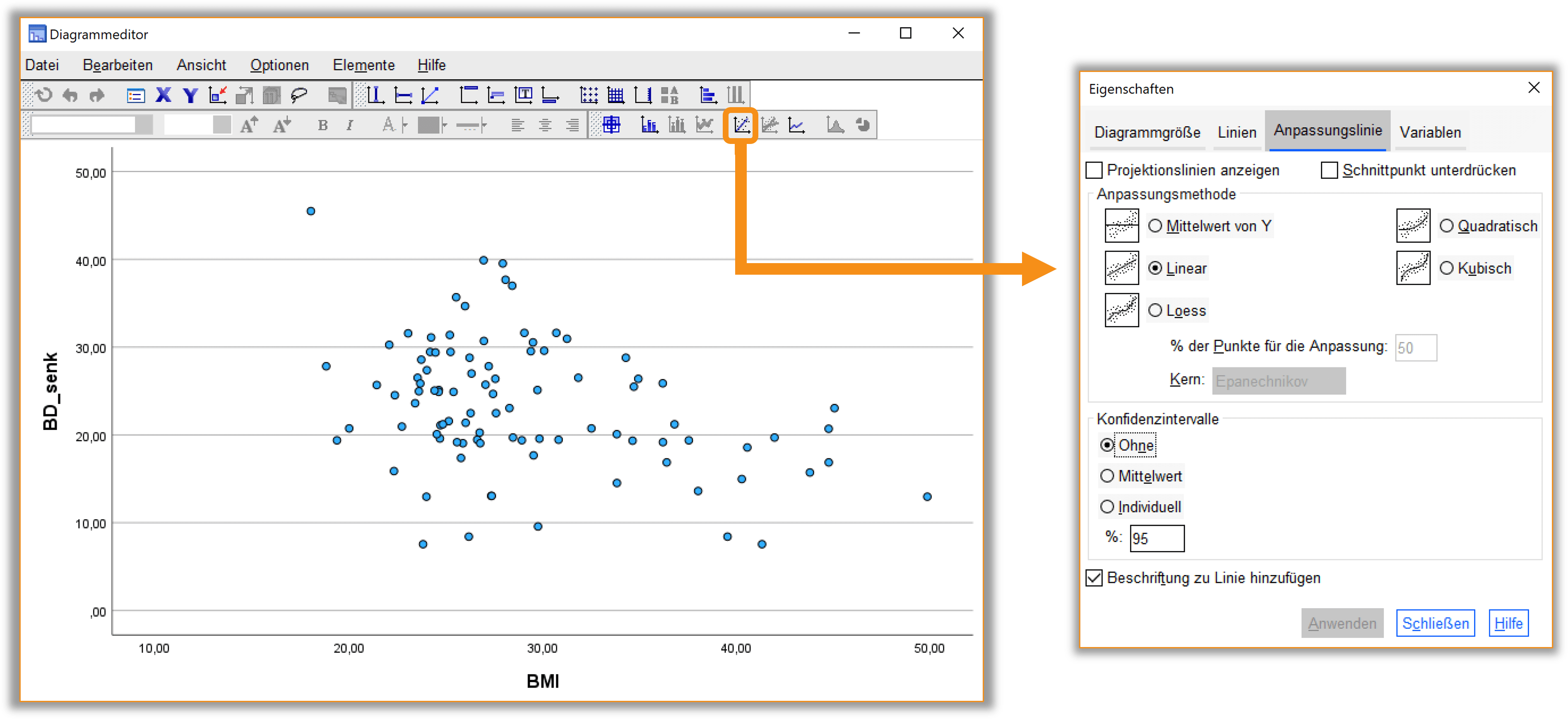
Schließen wir nun den Diagrammeditor beinhaltet unser Streudiagramm die berechnete lineare Regressionsgerade (vgl. Abb. 5).
Fußnoten
- 1Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2025), Universitätsklinikum Hamburg-Eppendorf.
- 2Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2025), Universitätsklinikum Hamburg-Eppendorf.
- 3Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2025), Universitätsklinikum Hamburg-Eppendorf.
- 4Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2025), Universitätsklinikum Hamburg-Eppendorf.
- 5Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2025), Universitätsklinikum Hamburg-Eppendorf.