t-Test in SPSS
Der t-Test für unabhängige Stichproben wird verwendet, um festzustellen, ob sich die Mittelwerte zwischen zwei Gruppen, deren Messwerte unabhängig voneinander sind, signifikant voneinander unterscheiden.
Beispiel "Blutdrucksenker"
Es soll untersucht werden, ob sich die mittlere Senkung des Blutdrucks nach den 5 Wochen Beobachtungszeit signifikant zwischen der Interventions- und der Kontrollgruppe unterscheidet. Somit wird die metrische Variable BD_senk als primärer Endpunkt betrachtet. Sie war annähernd normalverteilt in beiden Gruppen. Die nominale Variable gruppe legt als binäre Einflussvariable die Zuordnung zu Interventions- oder Kontrollgruppe fest.
Umsetzung in SPSS
Im SPSS-Menü: Analysieren » Mittelwerte und Proportionen vergleichen … » t-Test bei unabhängigen Stichproben …
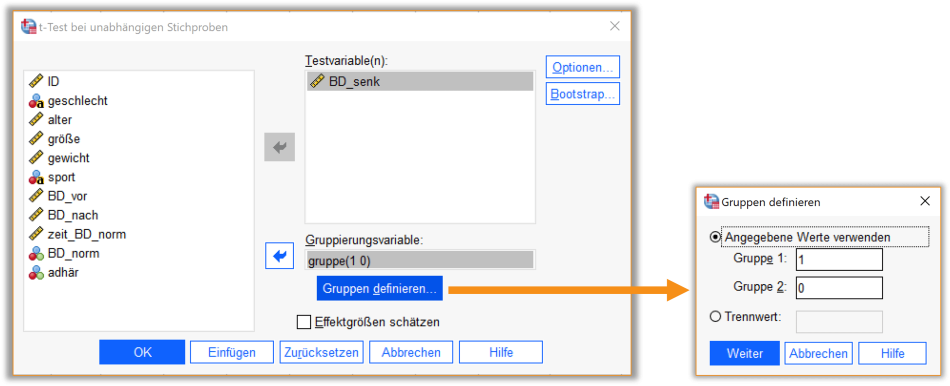
Als Testvariable wird das Outcome BD_senk und als Gruppierungsvariable gruppe verwendet (siehe Abb. 1). Über das Feld ‚Gruppen definieren‘ wird noch einmal spezifiziert, welche Ausprägung der Variable gruppe die Gruppe 1 bzw. 2 beschreiben soll. Wie in unserer manuellen Rechnung legen wir die Interventionsgruppe (gruppe=1) als Gruppe 1 und die Kontrollgruppe (gruppe=0) als Gruppe 2 fest.
Syntax
DATASET ACTIVATE DataSet1.
T-TEST GROUPS=gruppe(1 0)
/MISSING=ANALYSIS
/VARIABLES=BD_senk
/ES DISPLAY(TRUE)
/CRITERIA=CI(.95).
Interpretation des SPSS-Outputs
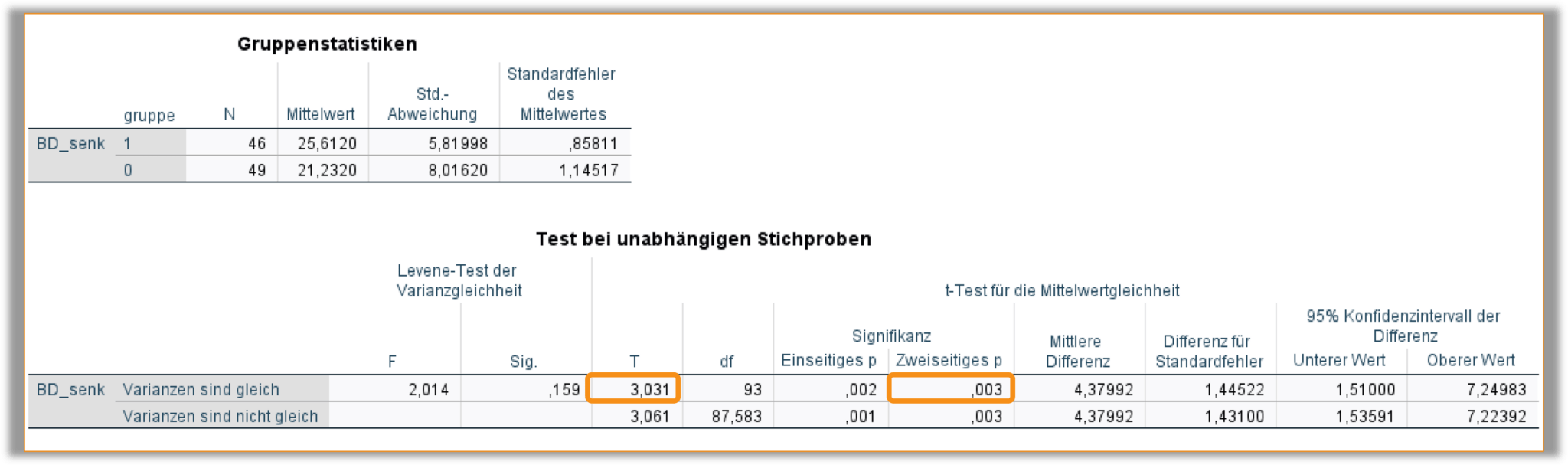
Der t-Test setzt neben der Normalverteilung der Daten auch Varianzhomogenität voraus. Zur Überprüfung der Normalverteilung dienen grafische Abbildungen, deren Erstellung in SPSS wir uns gesondert anschauen. Auch für die Überprüfung der Varianzhomogenität wird vom a-priori Test (der sogenannte Levene-Test, Spalte 1 und 2 der Testausgabe in Abb. 2) abgeraten.
Stattdessen vergleichen wir für die Annahme der Varianzhomogenität in der ersten Ausgabetabelle in Abb. 2 („Gruppenstatistiken“) die Standardabweichungen der zwei Gruppen. Bei einem relevanten Unterschied der Varianzen wird der p-Wert für ungleiche Varianzen (2. Zeile der Testtabelle, der sogenannte Welch-Test) zur Entscheidung herangezogen.
In diesem Beispiel wird der Unterschied der Standardabweichungen nicht als relevant eingestuft, also wird die obere Zeile der Testtabelle in Abb. 2 („Varianzen sind gleich“) betrachtet. Die Teststatistik wurde als T=3,031 berechnet. Der zugehörige zweiseitige p-Wert ergab p=0,003.
Da der p-Wert < 0,05 ist, gibt es einen signifikanten Unterschied zwischen Patient:innen der Interventionsgruppe (Gruppe 1) und Patient:innen der Kontrollgruppe (Gruppe 2) bezüglich der mittleren Senkung des Blutdrucks.
Je nach Version von SPSS wird zum Teil ein p-Wert von .000 in der Tabelle angegeben. Dieser Wert bedeutet nicht p=0, sondern p<0,001. Neuere Version von SPSS geben direkt <0,001 in der Tabelle an.
Der t-Test für abhängige Stichproben wird verwendet, um festzustellen, ob sich die Mittelwerte zwischen zwei Gruppen, deren Messwerte abhängig voneinander sind, signifikant voneinander unterscheiden. Die Messwerte sind z. B. dann abhängig voneinander, wenn bei jeder Versuchsperson zwei Messungen durchgeführt wurden. Die Ergebnisse der ersten Messung bilden dann die Gruppe 1 und die Ergebnisse der zweiten Messung die Gruppe 2.
Im Rahmen des EpiBioManuals wurde der t-Test für abhängige Stichproben nicht behandelt. Trotzdem wollen wir an dieser Stelle kurz auf die Umsetzung in SPSS eingehen.
Beispiel "Blutdrucksenker"
Es soll untersucht werden, ob sich der Blutdruck der Patient:innen vor und nach der Intervention mit einem Medikament (es wird für dieses Beispiel ignoriert, ob es sich um die neue Intervention oder die Standardtherapie handelt) signifikant voneinander unterscheidet. Somit liegen für jede:n Patient:in zwei voneinander abhängige Ergebnisse vor, die die metrischen Variablen BD_vor und BD_nach ergeben. Die Mittelwerte dieser Variablen sollen miteinander verglichen werden. Die Differenzen der Variablen sind in der Variable BD_senk festgehalten, die wir bereits als annähernd normalverteilt beschrieben haben.
Umsetzung in SPSS
Im SPSS-Menü: Analysieren » Mittelwerte und Proportionen vergleichen … » t-Test bei Stichproben mit paarigen Werten …
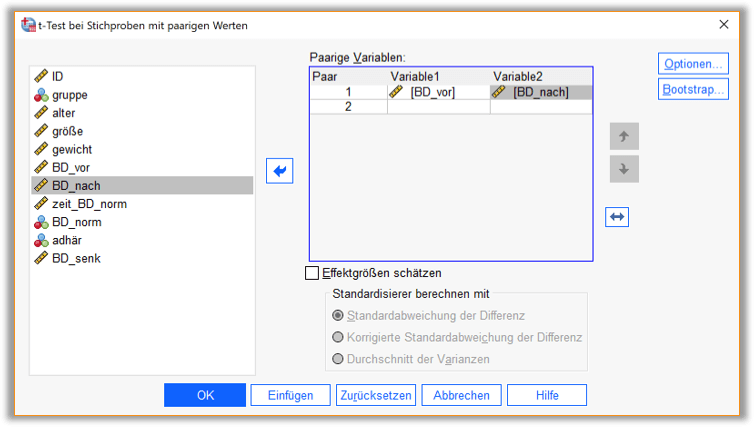
Im Dialogfenster (vgl. Abb. 1) werden die zwei betrachteten Variablen BD_vor und BD-nach als Paar eingefügt.
Syntax
DATASET ACTIVATE DataSet1.
T-TEST PAIRS=BD_vor WITH BD_nach (PAIRED)
/ES DISPLAY(FALSE)
/CRITERIA=CI(.9500)
/MISSING=ANALYSIS.
Interpretation des SPSS-Outputs
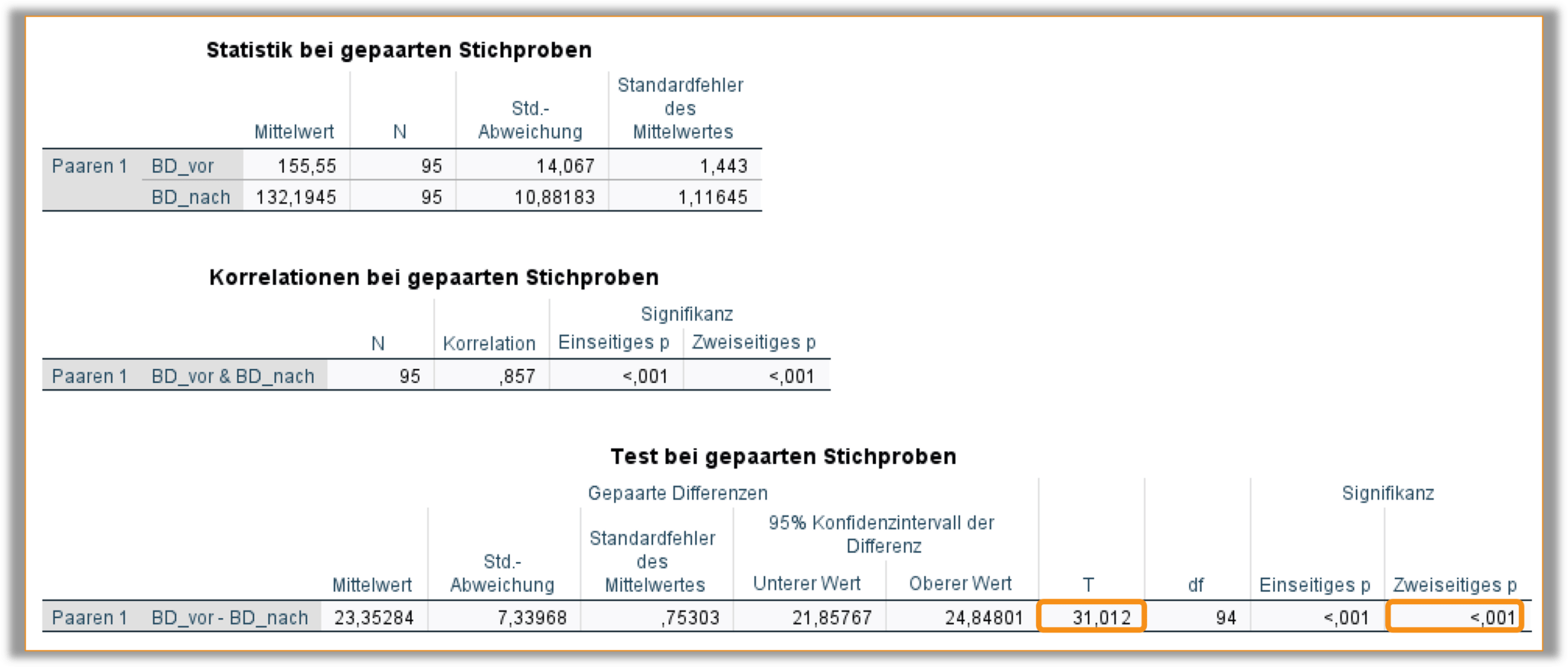
Während in Abb. 2 die zwei oberen Tabellen („Statistik bei gepaarten Stichproben“ und „Korrelationen bei gepaarten Stichproben“) erste deskriptive Erkenntnisse der beiden Variablen und ihre Korrelation untereinander zeigen, sind die für uns relevanten Testergebnisse in der unteren Teststabelle abgebildet.
Die Teststatistik ergab T=31,012. Der zugehörige zweiseitige p-Wert ist p<,001.
Da der p-Wert < 0,05 ist, gibt es einen signifikanten Unterschied zwischen dem Blutdruck der Patient:innen vor und nach der Intervention durch ein Blutdruck senkendes Medikament.
Der Ein-Stichproben-t-Test wird verwendet, um festzustellen, ob sich der Mittelwert einer Stichprobe signifikant von einem Referenzwert (z. B. einem Standardwert) unterscheidet.
Im Rahmen des EpiBioManuals wurde der Ein-Stichproben-t-Test nicht behandelt. Trotzdem wollen wir an dieser Stelle kurz auf die Umsetzung in SPSS eingehen.
voraussetzungen
- Messungen stammen aus einer zufällig gezogenen Stichprobe
- Outcome ist metrisch skaliert und annähernd normalverteilt
Beispiel "Blutdrucksenker"
Es soll untersucht werden, ob sich der mittlere Blutdruck aller Patient:innen der Zufallsstichprobe vor der medikamentösen Intervention signifikant vom Normwert des systolischen Blutdrucks (Annahme: 120 mmHg) unterscheidet. Somit wird die metrische Variable BD_vor betrachtet. Wir gehen von einer annähernden Normalverteilung der Variablen aus.
Umsetzung in SPSS
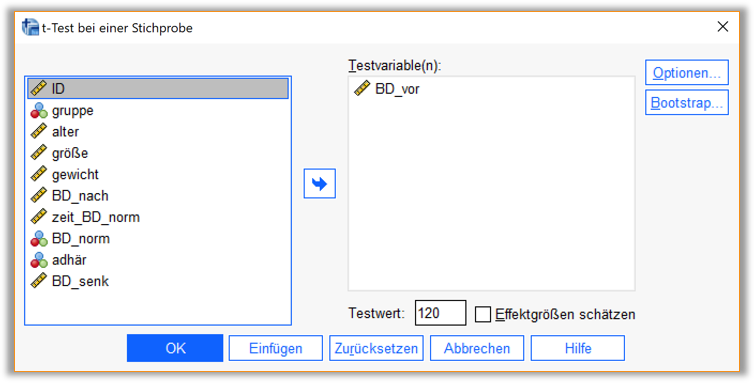
Im SPSS-Menü: Analysieren » Mittelwerte und Proportionen vergleichen … » t-Test bei einer Stichprobe …
Als Testvariable wird zunächst die Variable BD_norm eingetragen (siehe Abb. 1). In das Feld ‚Testwert‘ wird der Wert eingetragen, mit dem der Mittelwert verglichen werden soll – in unserem Fall also 120.
Syntax
DATASET ACTIVATE DataSet1.
T-TEST
/TESTVAL=120
/MISSING=ANALYSIS
/VARIABLES=BD_vor
/ES DISPLAY(FALSE)
/CRITERIA=CI(.95).
Interpretation des SPSS-Outputs
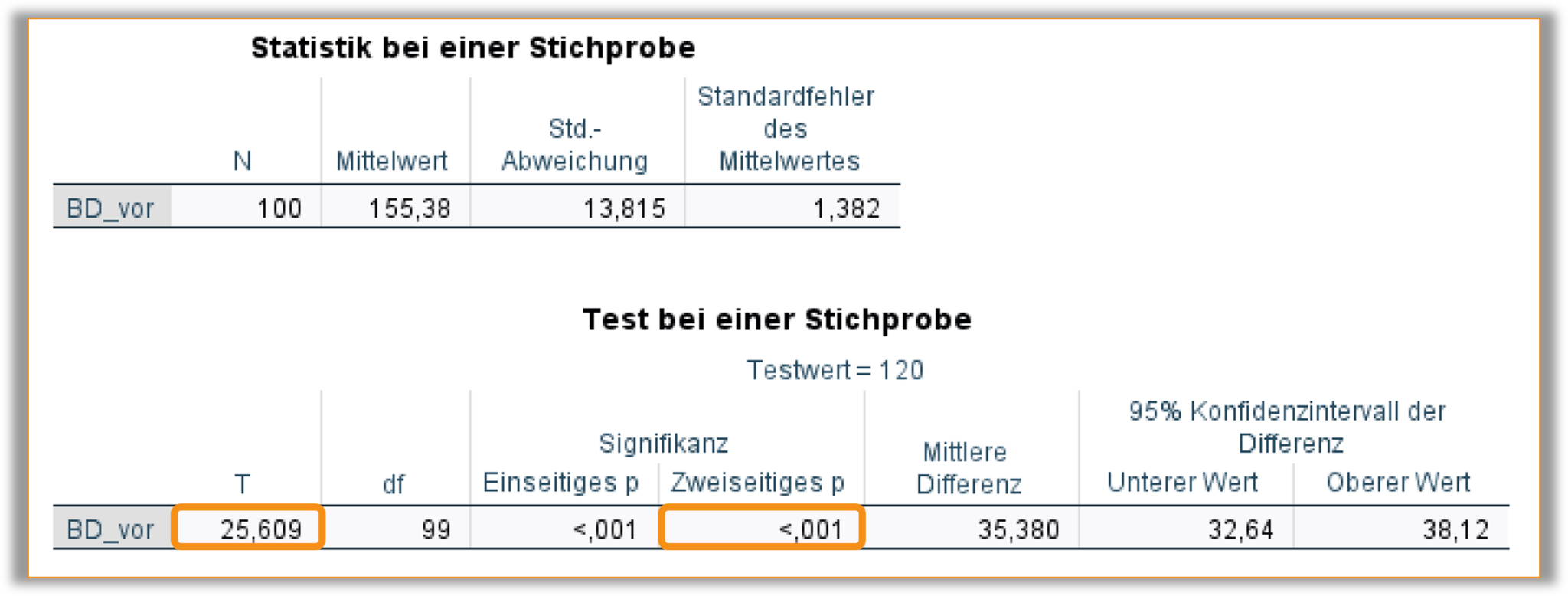
In Abb. 2 ist der Output des Ein-Stichproben-t-Tests abgebildet.
Die Teststatistik wurde als T=25,609 berechnet. Der zugehörige zweiseitige p-Wert ist p<0,001.
Da der p-Wert < 0,05 ist, konnte ein signifikanter Unterschied des Stichprobenmittelwerts vom Normwert des systolischen Blutdruck 120 mmHg festgestellt werden. Da wir im EpiBioManual ausschließlich beidseitige Tests betrachten, kann genau genommen keine Aussage darüber getroffen werden, in welche Richtung dieser Unterschied vorliegt. Der Mittelwert der Stichprobe liegt mit 155,38 mmHg allerdings deutlich über dem Normwert, sodass von einem mittleren erhöhten Blutdruck in der Stichprobe ausgegangen werden kann.
Fußnoten
- 1Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2024), Universitätsklinikum Hamburg-Eppendorf.
- 2Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2024), Universitätsklinikum Hamburg-Eppendorf.
- 3Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2024), Universitätsklinikum Hamburg-Eppendorf.
- 4Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2024), Universitätsklinikum Hamburg-Eppendorf.
- 5Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2024), Universitätsklinikum Hamburg-Eppendorf.
- 6Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2024), Universitätsklinikum Hamburg-Eppendorf.