Deskriptive Statistik
Studienauswertung
Wie bereits erläutert, versucht die deskriptive Statistik, die Daten der Stichprobe zu beschreiben und darzustellen. Dies ist sinnvoll um einerseits die Repräsentativität der Stichprobe zu überprüfen und andererseits, um einen ersten Überblick über die Daten zu erhalten.
Die deskriptive Statistik umfasst verschiedene Kenngrößen und grafische Darstellungen. Welche Methoden für die jeweiligen Variablen geeignet sind, hängt von ihrem Skalenniveau und ihrer Verteilung ab. Die bekannteste Verteilung, die für viele statistische Verfahren auch annähernd vorausgesetzt wird, ist die Normalverteilung. Sie wird neben der t-Verteilung und der Chi-Quadrat-Verteilung im Abschnitt Verteilungen behandelt.
In diesem Abschnitt im Kapitel „deskriptive Statistik“ werden die wichtigsten statistischen Kenngrößen vorgestellt.
Es wird zwischen Punktschätzern und Streuungsschätzern unterschieden.
Punktschätzer
Ein Punktschätzer schätzt einen unbekannten Parameter der Grundgesamtheit durch einen einzigen Wert. Als Basis für die Schätzung werden die Daten aus der Stichprobe herangezogen. Im Folgenden werden die wichtigsten Punktschätzer vorgestellt.
Absolute und Relative Häufigkeiten
Absolute Häufigkeiten messen die aufsummierten Vorkommnisse einer Beobachtung (z. B. „Wie viele Personen …?“ oder „Wie oft ist ein bestimmtes Ereignis eingetreten?“).
Relative Häufigkeiten bilden dazu die Ergänzung. Sie setzen die absolute Anzahl einer bestimmten Beobachtung/eines Ereignisses in Relation zur Gesamtanzahl aller Beobachtungen/Ereignisse. Die relativen Häufigkeiten ergeben in Summe 1 (bzw. 100%).
Häufigkeiten sind isoliert betrachtet oft irreführend, weshalb sie meist nebeneinander angeschaut werden, wie im Beispiel verdeutlicht wird.
Beispiel "Blutdrucksenker"
| Beobachtungsvariable | Absolute Häufigkeit (relative Häufigkeit in %) | ||
|---|---|---|---|
| Teilnehmende | Interventionsgruppe | Kontrollgruppe | Total |
|
34 (68) | 30 (60) | 64 (64) |
|
16 (32) | 20 (40) | 36 (36) |
Negativbeispiel
|
Beobachtungsvariable |
||
|---|---|---|
|
Teilnehmende |
Kontrollgruppe (n=500) |
Interventionsgruppe (n=1000) |
|
7 (1,4) |
14 (1,4) |
Mittelwert
Der wohl bekannteste Punktschätzer ist der Mittelwert \bar {x} als Schätzer für den Erwartungswert \mu, also das tatsächliche Mittel, der Grundgesamtheit. Er beschreibt den Durchschnittswert über alle Beobachtungen hinweg. Der Mittelwert wird mithilfe der folgenden Formel berechnet:
\bar{x}=\frac{1}{n}\cdot \sum_{i=1}^n{x_i}
Mit dem Buchstaben n wird dabei die Anzahl an Beobachtungen beschrieben. Es wird also die Summe über alle Beobachtungen hinweg berechnet und dann durch die Anzahl an Beobachtungen geteilt.
Beispiel "Blutdrucksenker"
Weist die Variable Körpergröße z. B. die Beobachtungen 170 cm, 182 cm, 191 cm, 170 cm, 168 cm, 157 cm, 178 cm, 195 cm, 162 cm und 185 cm (vereinfacht werden nur 10 der 100 Patient:innen in der Beispielstudie betrachtet) auf, ist der Mittelwert durch \frac{1}{10}\cdot (170 \text{ cm}+182 \text{ cm}+191 \text{ cm}+170 \text{ cm}+168 \text{ cm}+157 \text{ cm}+178 \text{ cm}+195 \text{ cm}+162 \text{ cm}+185 \text{ cm}) = 175,8 \text{ cm} gegeben.
Median
Ein weiterer Punktschätzer ist der Median x_Med. Er ist der Wert, der in der Mitte der Beobachtungen liegt und wird deshalb auch häufig als “Zentralwert” bezeichnet. 50 % der Beobachtungen haben also einen Merkmalswert größer oder gleich bzw. kleiner oder gleich dem Median. Um den Median zu ermitteln, werden im ersten Schritt die Beobachtungen nach ihrer Größe sortiert und dann mithilfe einer der folgenden Formeln der Median bestimmt:
| für ungerade | x_{Med}=x_{(\frac{n+1}{2})} |
| für gerade | x_{Med}=\frac{x_{(\frac{n}{2})}+x_{(\frac{n}{2}+1)}}{2} |
Übrigens: der Mittelwert und der Median können in einigen Fällen auch den gleichen Wert annehmen. Ein Vorteil des Medians gegenüber dem Mittelwert ist, dass er weniger anfällig für Ausreißer ist.
Beispiel "Blutdrucksenker"
In unserem Beispiel sind die Größen sortiert 157 cm, 162 cm, 168 cm, 170 cm, 170 cm, 178 cm, 182 cm, 185 cm, 191 cm, 195 cm. Da und somit gerade ist, ist der Median der Mittelwert der zwei Beobachtungen in der Mitte der Reihe der sortierten Körpergrößen also x_{Med}=\frac{x_{5}+x_{6}}{2}=\frac{170\text{ cm}+178\text{ cm}}{2}=174\text{ cm}. Gäbe es noch eine weitere größere Beobachtung x_{11}=196\text{ cm}, könnten wir einfach den Wert in der Mitte der Beobachtungen raussuchen und bestimmen den Median mit x_{Med}=x_{6}=178\text{ cm}.
Zusatzwissen
Modalwert
Außerdem betrachtet die deskriptive Statistik häufig den Modalwert. Der Modalwert (oder auch Modus) ist der Wert, der in den Beobachtungen der Stichprobe am häufigsten vorkommt. In unserem Beispiel also die Körpergröße 170 cm, da diese als einzige zwei Mal in den Beobachtungen vorkommt.
Es gibt immer einen Modus, allerdings muss er nicht eindeutig sein, d.h. es können auch mehrere Werte Modalwert sein.
Quantile und Quartile
Ein weiteres Lagemaß sind Quantile, die die sortierten Beobachtungen der Stichprobe unterteilen. Das p-Quantil einer Stichprobe beschreibt den Wert, unter dem sich p-Prozent der Stichprobenwerte befinden. Quartile sind besondere Quantile und teilen die Beobachtungen der Stichprobe in vier gleich große Teile. Das erste Quartil Q1 oder auch 25 %-Quantil sagt aus, dass 25 % der Stichprobenwerte kleiner oder gleich Q1 sind. Es werden typischerweise das 25 %- (Q1), das 50 %- (Q2, entspricht dem Median) und das 75 %-Quantil (Q3) betrachtet.
Beispiel "Blutdrucksenker"
Schauen wir uns wieder unser Beispiel mit den Körpergrößen an und sortieren sie nach der Größe, also 157 cm, 162 cm, 168 cm, 170 cm, 170 cm, 178 cm, 182 cm, 185 cm, 191 cm, 195 cm. Wir sehen, dass die 25 %-Marke der Beobachtungen bei einer Körpergröße von 168 cm (Q1) erstmals überschritten wird. Das heißt, dass 25 % der zehn betrachteten Patient:innen eine Körpergröße kleiner oder gleich 168 cm aufweisen. Die 50 %-Marke wird bei 174 cm (Q2, siehe auch Median) und die 75 %-Marke bei 185 cm (Q3) überschritten. Um das Konzept der Quartile noch besser zu verstehen, kann es hilfreich sein, geeignete deskriptive grafische Darstellungen zu betrachten.
Beispiel "Blutdrucksenker"
Die sortierten Körpergrößen in unserem Beispiel sind 157 cm, 162 cm, 168 cm, 170 cm, 170 cm, 178 cm, 182 cm, 185 cm, 191 cm, 195 cm. Somit ist 157 cm die minimale und 195 cm die maximale Körpergröße in den Beobachtungen der Stichprobe.
Ereigniszeitdaten
Als nächstes widmen wir uns den deskriptiven Kenngrößen im Zusammenhang mit der Ereigniszeitanalyse. Da historisch betrachtet häufig der Tod von Patient:innen betrachtet wurde und die Zeit bis dahin von Interesse war, wird auch heute oft noch von einer Analyse der „Überlebenszeit“ gesprochen. Die Kenngrößen der Ereigniszeitanalyse können am einfachsten mit Hilfe von grafischen Methoden, wie der Kaplan-Meier-Kurve, ermittelt werden. Wir empfehlen euch deshalb für ein besseres Verständnis, diesen Abschnitt hier direkt in Kombination mit der Erklärung zu den grafischen Methoden der Ereigniszeitanalyse anzuschauen.
Die erste betrachtete Kenngröße der Ereigniszeitanalyse ist die Ereignisrate. Diese misst die relative Häufigkeit, mit der ein bestimmtes Ereignis in der Stichprobe innerhalb eines Zeitraums eingetreten ist. Die Wahrscheinlichkeit, dass das betrachtete Ereignis bis zu einem bestimmten Zeitpunkt nicht eintritt unter Berücksichtigung von zensierten Daten, wird durch den sogenannten Kaplan-Meier-Schätzer geschätzt. Wie dieser genau ermittelt wird, werdet ihr im Abschnitt zur Kaplan-Meier-Kurve lernen.
Beispiel "Blutdrucksenker"
In unserem Beispiel konnten bis zum Studienende nach 5 Wochen bei 32 von 50 Patient:innen der Kontrollgruppe der Blutdruck vom erhöhten in den Normbereich ( < 140 mmHg) abgesenkt werden. Die Ereignisrate beträgt somit 64 %, da bei 64 % der Patient:innen der Kontrollgruppe das Ereignis „Blutdruck ist wieder in den Normbereich gesunken“ im Studienverlauf eingetreten ist.
Die Personen unter Risiko (engl.: Number at Risk) geben an, wie viele der Patient:innen zu einem bestimmten Zeitpunkt t einem Ereignisrisiko ausgesetzt sind. Wenn der Tod als Ereignis betrachtet wird, handelt es sich also um genau die Patient:innen, die am Zeitpunkt t weder bereits gestorben noch zensiert sind. Die Angabe der Personen unter Risiko ist eine Orientierung dafür, wie aussagekräftig die Kaplan-Meier-Schätzung am rechten Rand der Verteilung (wenn nur noch wenige Patient:innen unter Ereignisrisiko stehen) noch ist.
Beispiel "Blutdrucksenker"
Die Bezeichnung „Personen unter Risiko“ ist in Bezug auf unser Beispiel ein wenig missverständlich, da wir im Vergleich zum historisch betrachteten Ereignis „Tod“ ein positiv bewertetes Ereignis, nämlich „Blutdruck ist wieder in den Normbereich gesunken“, betrachten. Wir schauen uns also an, wie viele Personen zu einem bestimmten Zeitpunkt t innerhalb des Studienverlaufs dem „Risiko“ ausgesetzt sind, dass ihr Blutdruck in nächster Zeit in den Normbereich gesenkt wird: Das sind die Teilnehmenden, deren Blutdruck bisher noch nicht im Normbereich liegt, die aber weiterhin unzensiert an der Studie teilnehmen, also noch nicht frühzeitig ausgeschieden sind. In unserer Kontrollgruppe sind dies am Zeitpunkt t=14, also nach zwei Wochen, beispielsweise noch 38 Versuchspersonen von den insgesamt 50 Teilnehmer:innen (siehe dazu die später erläuterte Tabelle zur Kaplan-Meier-Kurve.)
Die mediane Ereigniszeit gibt den Zeitpunkt an, an dem bei genau der Hälfte der Patient:innen das betrachtete Ereignis eingetreten ist. Da wie gesagt häufig der Tod als eintretendes Ereignis untersucht wurde, sprach man im Gegensatz zum Tod vom Überleben der Patient:innen und die Kenngröße wird häufig auch als mediane Überlebenszeit bezeichnet. Es wird eher die mediane anstelle der mittleren Ereigniszeit betrachtet, da diese bereits angegeben werden kann, sobald das Ereignis bei der Hälfte der Patient:innen eingetreten ist. Für die mittlere Ereigniszeit müsste man erst den Eintritt des Ereignisses bei allen Patient:innen abwarten. Sie ist somit auch abhängig vom jeweiligen Zensierungsmuster.
Beispiel "Blutdrucksenker"
In unserer Kontrollgruppe konnte z. B. nach 30 Tagen bei 25 Patient:innen (von 50 Patient:innen der Kontrollgruppe) der Blutdruck in den Normbereich gesenkt werden. Somit beträgt die mediane Ereigniszeit in der Kontrollgruppe 30 Tage. Am einfachsten könnt ihr die mediane Ereigniszeit mithilfe einer Kaplan-Meier-Kurve ablesen, was an späterer Stelle erklärt wird.
Streuungsschätzer
Die Streuungsschätzer dienen dazu, Punktschätzer einzuordnen und, ähnlich wie im Fall der absoluten und relativen Häufigkeiten, ein Gesamtbild zu schaffen. Ein Mittelwert der Körpergröße von 170 cm sagt alleine wenig über eine Stichprobe aus, ohne auch die Streuung der Beobachtungen um ihn herum zu betrachten.
Beispiel "Blutdrucksenker"
Die Datenreihe mit den Körpergrößen 157 cm, 162 cm, 168 cm, 170 cm, 170 cm, 178 cm, 182 cm, 185 cm, 191 cm, 195 cm weist den gleichen Mittelwert wie die Datenreihe 127 cm, 132 cm, 138 cm, 140 cm, 140 cm, 208 cm, 212 cm, 215 cm, 221 cm, 225 cm auf, wenn sie auch vollkommen unterschiedliche Sachverhalte beschreiben – bei der ersten Datenreihe handelt es sich nämlich um eine Stichprobe von erwachsenen Menschen, bei der zweiten um die Größe von Starwars-Charakteren. Wird nur der Mittelwert alleine berichtet, fällt dies gar nicht auf.
Spannweite und Interquartilsabstand
Zwei Maßzahlen, um die Spanne zu betrachten, in der sich die Beobachtungen bewegen, sind die Spannweite (Range) und der Interquartilsabstand (IQR, engl.: Interquartile Range). Die Spannweite wird durch die Differenz zwischen Maximum und Minimum berechnet. Der Interquartilsabstand beschreibt, wie der Name bereits vermuten lässt, den Abstand zwischen dem 25%- und dem 75%-Quartil.
Beispiel "Blutdrucksenker"
In unserem Beispiel mit den sortierten Körpergrößen 157 cm, 162 cm, 168 cm, 170 cm, 170 cm, 178 cm, 182 cm, 185 cm, 191 cm, 195 cm lässt sich die Spannweite also durch \text{Max}-\text{Min}= 195\text{ cm}-157 \text{ cm}=38 \text{ cm} berechnen.
Die IQR kann durch \text{Q3}-\text{Q1}=185\text{ cm}-168\text{ cm}=17\text{ cm} ermittelt werden.
Varianz und Standardabweichung
Die wohl am häufigsten betrachteten Streuungsmaße sind die Varianz und die Standardabweichung der Stichprobe. Die Stichprobenvarianz wird berechnet durch
Var(x)=SD(x)^2=\frac{1}{n-1} \cdot \sum_{i=1}^n{(x_i-\bar{x})^2}
und beschreibt somit die quadrierte durchschnittliche Entfernung vom Mittelwert der Stichprobe. Durch das Quadrieren hat sie eine andere Maßeinheit als die ursprünglichen Beobachtungen, sodass eine Interpretation des Wertes schwierig ist und eher die Standardabweichung der Stichprobe betrachtet werden sollte: Sie beschreibt die durchschnittliche Streuung der einzelnen Ausprägungen um den beobachteten Mittelwert und wird aus der Wurzel der Stichprobenvarianz berechnet:
SD(x)=\sqrt{Var(x)}=\sqrt{\frac{1}{n-1} \cdot \sum_{i=1}^n{(x_i-\bar{x})^2}}
Beispiel "Blutdrucksenker"
Sehen wir uns nun ein Beispiel an: Wir kennen bereits den Mittelwert \bar{x}=175,8\text{ cm}. Für die Stichprobenvarianz berechnen wir Var(x)=\frac{1}{9} \cdot ((157-175,8)^2+ (162-175,8)^2+ (168-175,8)^2+ (170-175,8)^2+ (170-175,8)^2+(178-175,8)^2+ (182-175,8)^2+(185-175,8)^2+ (191-175,8)^2+ (195-175,8)^2 ) \approx 155,51 und für die Standardabweichung der Stichprobe SD(x)=\sqrt{Var(x)}\approx 12,47 \text{ cm}. D. h. im Durchschnitt streut die Körpergröße in unserer Stichprobe ca. 12,5 cm um den Mittelwert.
Zusatzwissen
Warum teilen wir durch (n-1)?
Wenn wir die Varianz oder Standardabweichung der Stichprobe berechnen wollen (und eben nicht die Daten der Grundgesamtheit vorliegen haben und daraus direkt Standardabweichung und Varianz berechnen können), müssen wir statt durch n durch n-1 teilen. Dieser Schritt wird als „Bessel-Korrektur” bezeichnet und ist notwendig, damit der Streuungsschätzer nicht zu klein geschätzt wird. Die „Unterschätzung” der Streuung der Stichprobe beim Teilen durch n kommt zustande, da wir für die Berechnung der Stichprobenvarianz bzw. Standardabweichung auch nur den Mittelwert der Stichprobe \bar{x} benutzen, welcher nur ein Schätzer vom tatsächlichen Mittelwert darstellt und so für eine systematische Verzerrung sorgt.
Wenn du willst, schaue dir ein hilfreiches Video bei YouTube zu diesem Thema an.
Standardfehler
Ein weiteres Streuungsmaß ist der Standardfehler, der die Streuung des Schätzers selbst betrachtet. Der Standardfehler des Mittelwerts gibt an, wie groß die durchschnittliche Abweichung des geschätzten Mittelwerts der Stichprobe vom tatsächlichen Mittelwert in der Grundgesamtheit ist. Da der tatsächliche Mittelwert der Grundgesamtheit meist für uns unbekannt ist, gilt es auch den Standardfehler zu schätzen. Das ist mithilfe der folgenden Formel möglich:
SE=\frac{SD(x)}{\sqrt{n}}.
Beispiel "Blutdrucksenker"
Für unser Beispiel ergibt sich ein Standardfehler von SE \approx \frac{12,47}{\sqrt{10}} \approx 3,94. Das heißt wir schätzen eine durchschnittliche Abweichung des geschätzten Mittelwerts der Körpergrößen unserer Stichprobe vom tatsächlichen Mittelwert der Körpergrößen der Grundgesamtheit (also der an Bluthochdruck leidenden erwachsenen Bevölkerung) von 3,94 cm.
LITERATURVERZEICHNIS
Die Inhalte dieses Abschnitts sind angelehnt an:
In diesem Abschnitt sollen grundlegende Grafiken, die in der deskriptiven Statistik häufig Anwendung finden, vorgestellt werden. Wann welche Abbildung sinnvoll ist, hängt davon ab, welches Skalenniveau die Variable aufweist. Es gibt auch grafische Methoden für die simultane Darstellung zweier (oder mehr) Variablen, wie z. B. das später behandelte Streudiagramm.
Beispiel "Blutdrucksenker"
Da sich alle Grafiken dieses Abschnitts auf unser Beispiel zum Blutdruck senkenden Medikament beziehen, wird in diesem Kapitel auf die orangen Beispielkästen verzichtet.
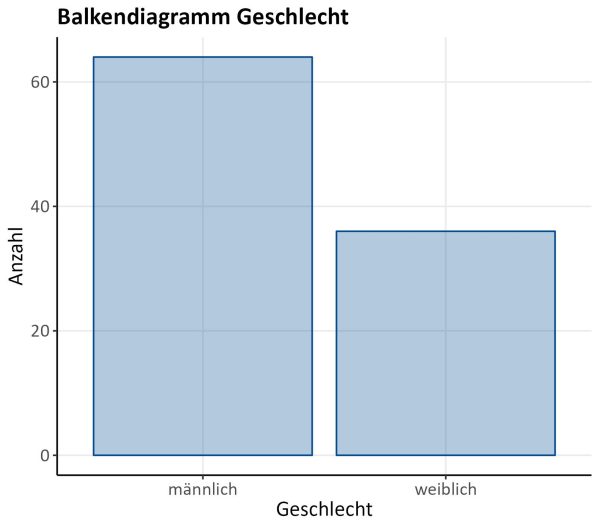
Balkendiagramm
Das Balkendiagramm (siehe Abb. 1) ist nützlich, um die Häufigkeiten der Ausprägungen einer kategorialen Variablen untereinander zu vergleichen. In der Grafik können auf der y-Achse entweder absolute oder relative Häufigkeiten in Prozent abgebildet werden.
Boxplot
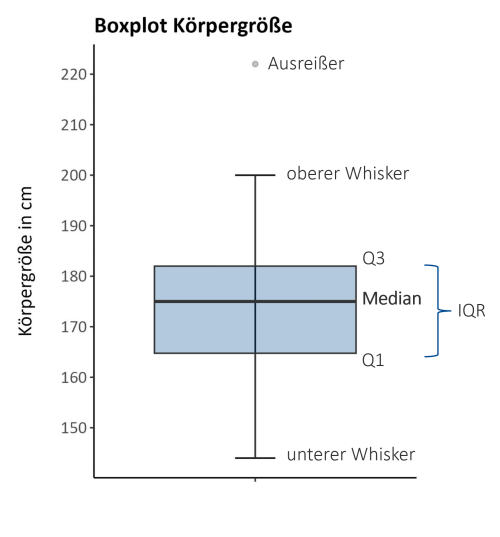
Ein Boxplot (siehe Abb. 2) ermöglicht es, mehrere Kenngrößen einer mindestens ordinal skalierten Variablen in einer Grafik darzustellen (von oben nach unten): Ausreißer nach oben (dargestellt als Punkte), oberer Whisker, 75%-Quantil (Q3), Median (Q2), 25%-Quantil (Q1), unterer Whisker, vermeintliche Ausreißer nach unten (keine vorhanden).
Die Whisker bieten eine grobe visuelle Möglichkeit, um die Anzahl extremer Werte in den Daten einzuschätzen und werden üblicherweise mit \text{Q}1 – 1,5 \cdot \text{IQR} bzw. \text{Q}3 + 1,5 \cdot \text{IQR} berechnet. Eine Ausnahme bietet der Fall, dass diese Werte Minimum und/oder Maximum übersteigen, sodass stattdessen diese als Whisker verwendet werden.
Während der Prüfung der Datenqualität haben wir uns den einzigen Ausreißer einmal genauer angeschaut: Es handelt sich um eine Frau mit einer vermeintlichen Körpergröße von 222 cm. Da die größte Frau der Welt laut Guinness Buch der Rekorde 215,16 cm groß ist1WELT (2021) Guinness Buch der Rekorde: Rumeysa Gelgi ist die größte Frau der Welt. Online abrufbar unter https://www.welt.de/vermischtes/article234379494/Guinness-Buch-der-Rekorde-Rumeysa-Gelgi-ist-die-groesste-Frau-der-Welt.html, zuletzt abgerufen am 28.12.2023., konnte es sich bei dieser Angabe nur um einen Datenfehler handeln. Wir haben noch einmal die konkrete Akte der Patient:in betrachtet und festgestellt, dass es sich um einen Eingabefehler während der Digitalisierung der Daten gehandelt hat. Der entsprechende Datensatz wurde korrigiert – die korrekte Körpergröße der Frau beträgt 155 cm.
Histogramm
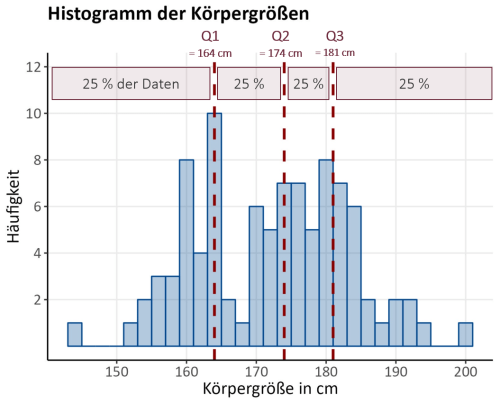
Histogramme dienen zur Abbildung der Verteilung von metrischen Variablen wie z. B. der Körpergröße in cm. Die Untersuchung zur Verteilung eines Merkmals ist dabei grundlegend notwendig zur weiteren Inferenz. Ein Histogramm sollte nicht mit einem Balkendiagramm verwechselt werden, auch wenn es auf den ersten Blick ähnlich erscheint. Im Vergleich zum Balkendiagramm werden die Beobachtungen erst bei Erstellung des Histogramms in selbst gewählte Gruppen eingeteilt. Durch diese Einteilung wird damit festgelegt, wie breit die Rechtecke des Histogramms werden. In unserem Beispiel (Abb. 3) haben wir drei Histogramme mit unterschiedlichen Klassenbreiten dargestellt: Wir sehen, dass alle 2 cm / 5 cm / 10 cm eine neue Klasse der Variable „Körpergröße“ beginnt. Je größer der Flächeninhalt der Rechtecke, desto mehr Versuchspersonen befinden sich in der jeweiligen Klasse der Körpergröße.

Ein Histogramm ist außerdem hilfreich, um das Konzept der Quartile besser zu verstehen: Sie teilen die Daten so ein, dass vier gleich große Teile entstehen. 25 % der Versuchspersonen unserer Stichprobe sind kleiner als Q1 (164 cm) und 75 % größer. 50% sind kleiner als Q2 (174 cm) und 50 % sind größer, sodass Q2 dem Median entspricht. Und schließlich sind 75 % der Versuchspersonen kleiner als Q3 (181 cm) und 25 % größer. Da wir nun die gesamte Stichprobe mit ihren 100 Versuchspersonen betrachten, unterscheiden sich die Werte von den oben genannten Berechnungen für die Quartile.
Empirische Verteilungsfunktion
Woher weiß man, ohne die genauen Daten zu betrachten, bei welcher konkreten Körpergröße sich das jeweilige Quartil befindet? Eine Abbildung, die hilfreich ist, um schnell die Quartile zu ermitteln, ist die sogenannte empirische Verteilungsfunktion, die unten (siehe Abb. 5) für die Körpergrößen aller 100 Versuchspersonen abgebildet ist. Ihr müsst nicht im Detail verstehen, was diese Grafik aussagt, sondern es genügt das Grundkonzept zu verstehen: Die Kurve zeigt stets an, wie viel Prozent der Stichprobe kleiner oder gleich der betrachteten Körpergröße ist. Je größer der Sprung ist, den die Gerade nach oben macht, desto mehr Patient:innen weisen genau den Wert der betrachteten Körpergröße auf. Das Q1 sagt beispielsweise aus, dass 25 % der Stichprobe kleiner als oder genau 164 cm groß sind.

Ereigniszeitdaten
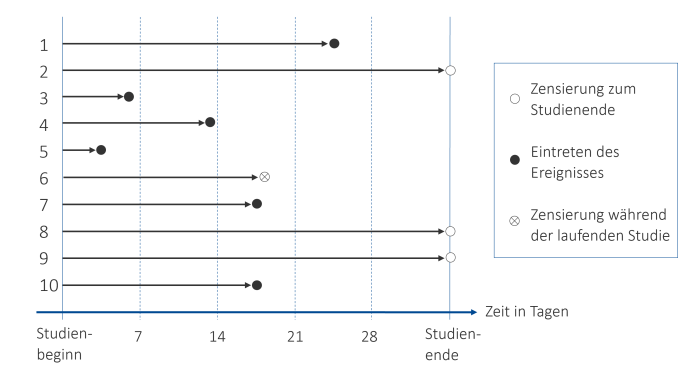
Die untenstehende Grafik (Abb. 6) ist eine gute Methode, um Ereigniszeitdaten von einzelnen Beobachtungen zu visualisieren. Wir betrachten hier unsere 10 Beispieldatensätze. Auf der x-Achse ist die Zeit von Studienbeginn bis Studienende der/s jeweiligen Patient:in in Tagen abgebildet. Im Laufe dieser Zeit tritt bei einigen Studienteilnehmer:innen das betrachtete Ereignis (hier der Punkt, an dem der systolische Blutdruck unter 140 mmHg sinkt) ein. Dieses Eintreten des Ereignisses ist mit dem schwarzen Punkt zu dem bestimmten Zeitpunkt markiert. Bei Versuchsperson Nr. 6 sehen wir einen besonderen Fall: Und zwar ist diese bereits vor regulärem Studienende aus der Studie ausgeschieden, was mit einem Punkt mit Kreuz gekennzeichnet ist. Die Beobachtungen 2, 8 und 9 waren bis zum regulären Studienende Teil der Untersuchung, aber haben das betrachtete Ereignis nie erreicht – ihr systolischer Blutdruck ist auch zu Studienende über 140 mmHg. In diesem Fall spricht man von (rechts-)zensierten Daten, da ihre weitere Entwicklung für die Forscher:innen nicht ersichtlich ist.
Kaplan-Meier-Kurve
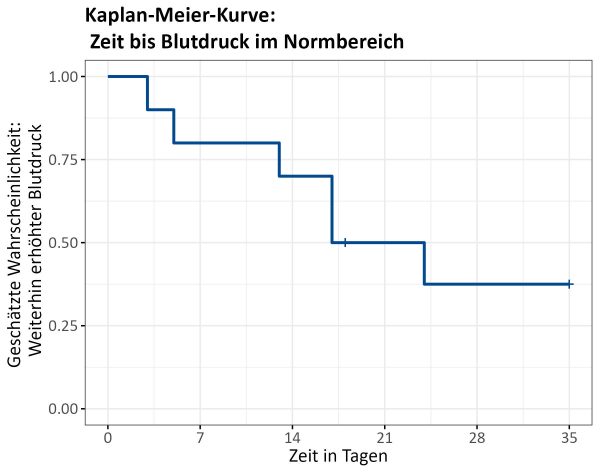
Wir wollen uns nun die sogenannte Kaplan-Meier-Kurve (manchmal auch empirische Überlebenskurve) für unsere Beispieldaten mit 10 Versuchspersonen anschauen (Abb. 7). Sie ist eine deskriptive Darstellung für Variablen auf der Ereigniszeitskala, bei der auch zensierte Daten geeignet berücksichtigt werden können. Auf der x-Achse ist der Zeitraum der Beobachtung (hier in Tagen) abgebildet – meistens von Studienbeginn bis Studienende (inkl. Nachbeobachtungszeit, wenn vorhanden). Die y-Achse reicht von 0 bis 1, da sie eine Wahrscheinlichkeit darstellt (1 = 100 %). Wird als Ereignis, wie häufig in der Praxis der Fall, der Tod der Patient:innen betrachtet, gibt ein Punkt auf der Kaplan-Meier-Kurve an, wie groß die geschätzte Überlebenswahrscheinlichkeit zu einem bestimmten Zeitpunkt (Kaplan-Meier-Schätzer) ist. Also die Wahrscheinlichkeit für ein Individuum, dass das betrachtete Ereignis nicht eintritt. In unserem Beispiel ist das betrachtete Ereignis das Sinken des Blutdrucks in den Normbereich ( < 140 mmHg). Damit zeigt die Kaplan-Meier-Kurve an, wie groß die geschätzte Wahrscheinlichkeit auf Basis unserer Stichprobendaten ist, zu einem bestimmten Zeitpunkt weiterhin unter einem erhöhten Blutdruck zu leiden.
| ID | Ereigniszeit: zeit_BD_norm | Status: BD_norm |
|---|---|---|
| 5 | 3 | 1 |
| 3 | 5 | 1 |
| 4 | 13 | 1 |
| 7 | 17 | 1 |
| 10 | 17 | 1 |
| 6 | 18 | 0 |
| 1 | 24 | 1 |
| 2 | 35 | 0 |
| 8 | 35 | 0 |
| 9 | 35 | 0 |
| 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|
| Ereigniszeit (t) | Anzahl Ereignisse zwischen t-1 und t (d) | Anzahl Zensierungen zwischen t-1 und t (q) | Personen unter Risiko zu t-1 (n) | 1-\frac{d}{n} | Kaplan-Meier-Schätzer |
| 0 | 0 | 0 | 10 | 1 | 1 |
| 3 | 1 | 0 | 10 | 0,9 | 0,9\cdot 1=0,9 |
| 5 | 1 | 0 | 9 | 0,89 | 0,89\cdot 0,9\approx 0,8 |
| 13 | 1 | 0 | 8 | 0,88 | 0,88\cdot 0,8\approx 0,71 |
| 17 | 2 | 0 | 7 | 0,71 | 0,71\cdot 0,71\approx 0,5 |
| 18 | 0 | 1 | 5 | – | – |
| 24 | 1 | 0 | 4 | 0,75 | 0,75\cdot 0,5\approx 0,38 |
| 35 | 0 | 3 | 3 | – | – |
Wir wollen nun auch die Kaplan-Meier-Kurve für unsere gesamten Daten mit 100 Patient:innen betrachten. Besonders interessant ist es, zwei Kaplan-Meier-Kurven für die beiden Behandlungsgruppen miteinander zu vergleichen. Diese sind hier in unterschiedlichen Farben dargestellt. Wir können auch die medianen Ereigniszeiten pro Gruppe ablesen: In der Interventionsgruppe sind nach 22 Tagen die Hälfte der Patient:innen mit ihrem systolischen Blutdruck in den Normbereich gesunken. In der Kontrollgruppe ist dies erst nach 30 Tagen der Fall. Durch das bloße Betrachten der Kurven könnte man vermuten, dass das neue Medikament eine bessere Blutdruck senkende Wirkung hat als die Standardtherapie. Ob sich die Kurven auch signifikant voneinander unterscheiden, kann erst durch weitere Untersuchungen (siehe dazu den später thematisierten Log Rank-Test) bestimmt werden.

LITERATURVERZEICHNIS
Die Inhalte dieses Abschnitts sind angelehnt an:
Normalverteilung
Die Normalverteilung ist vermutlich die bekannteste Verteilung in der Statistik. Da sie für die Auswahl der später thematisierten geeigneten Effektschätzer und viele Methoden der Inferenzstatistik eine wichtige Rolle spielt, soll sie hier genauer betrachtet werden.
Wie die Normalverteilung aussieht, wisst ihr vermutlich schon aus der Schule: Sie weist die typische „Glockenform“ auf, ist also unimodal, und ist symmetrisch um ihren wahren Mittelwert \mu verteilt. Ändern wir den Mittelwert, verschiebt sich die Verteilung entlang der x-Achse. Die tatsächliche Standardabweichung \sigma bestimmt, wie ihr ja bereits im Abschnitt Streuungsschätzer gelernt habt, wie stark die Werte um den Mittelwert streuen. Ein kleiner Wert für \sigma sorgt somit für eine gestauchte, also „flache“ Verteilung. In Abbildung 9 sind verschiedene Normalverteilungen für unterschiedliche Werte von \mu und \sigma abgebildet.

Die Standardnormalverteilung ist ein Sonderfall der Normalverteilung mit einem Mittelwert \mu=0 und der Standardabweichung \sigma=1 und deshalb in der Grafik dick (blaue Kurve) hervorgehoben.
Zusatzwissen
Z-Transformation zu einer Standardnormalverteilung
Eine normalverteilte Zufallsvariable lässt sich immer zu einer standardnormalverteilten Zufallsvariable transformieren. Dazu werden ihre Ursprungswerte durch die sogenannte Z-Transformation
Z = \frac{X-\mu}{\sigma},
also das Abziehen des Mittelwerts und das Dividieren durch die Standardabweichung, angepasst. Die Vorteile sind eine bessere Einordnung einzelner Messwerte im Bezug zu ihrem Erwartungswert \mu und die wünschenswerten Eigenschaften der Standardnormalverteilung.
Beispiel "Blutdrucksenker"
Viele metrische Variablen sind bei großer Stichprobengröße annähernd normalverteilt. Wir wollen uns genauer die aus den erhobenen Daten berechnete Variable BD_senk angucken, die die Differenz des systolischen Blutdrucks nach 5 Wochen (BD_nach) und dem Baselinewert (BD_vor) betrachtet. Ist diese annähernd normalverteilt? Wir werden auch im nächsten Abschnitt zu den Effektschätzern sehen, dass der Umgang mit metrischen Variablen davon abhängt, ob diese annähernd normalverteilt sind oder nicht. Deshalb ist diese Information für den weiteren Verlauf unserer Beispielstudie relevant.
Zur Überprüfung der Normalverteilung ist es hilfreich, deskriptive grafische Methoden zu betrachten. In der folgenden Abbildung 10 ist pro Behandlungsgruppe das Histogramm der Blutdrucksenkung mit der jeweilig zugehörigen Normalverteilung in dunkelrot eingezeichnet.

Die mittlere Blutdrucksenkung in der Kontrollgruppe beträgt ungefähr 21 mmHg für den systolischen Blutdruck, während er in der Interventionsgruppe bei ca. 26 mmHg liegt. Um diese Werte sind die Normalverteilungen jeweils zentriert. Ihre Breite wird durch die empirische Standardabweichung der Variablen pro Gruppe beschrieben, die in der Kontrollgruppe ca. 8 mmHg und in der Interventionsgruppe ca. 6 mmHg beträgt. Das heißt die gemessenen Differenzen der Blutdruckwerte schwanken im Mittel mit 8 mmHg bzw. 6 mmHg um die mittlere Senkung von 21 mmHg bzw. 26 mmHg.
Wir sehen in den Grafik der Kontrollgruppe, dass nur wenige Proband:innen eine Blutdrucksenkung von weniger als 13 mmHg (21 mmHg – 8 mmHg) und mehr als 29 mmHg (21 mmHg + 8 mmHg) hatten. Der größte Teil der Proband:innen liegt in der Mitte der Verteilung. Wären die Daten perfekt an die Normalverteilung angepasst, würden in dem Bereich zwischen 13 mmHg und 29 mmHg genau 68 % der Beobachtungen liegen (aufgrund der speziellen Form der Normalverteilung). In der Interventionsgruppe liegt dieser Bereich zwischen 20 mmHg und 32 mmHg (26 mmHg ± 6 mmHg).
Wir sehen allerdings in den Grafiken, dass die Daten der Stichprobe nicht optimal an die Normalverteilung angepasst sind und dass in beiden Gruppen auffällig viele Beobachtungen um die 20 mmHg liegen. Vielleicht handelt es sich um eine zufällige Häufung in diesem Bereich, die bei größerer Stichprobe nicht mehr auftreten würde – vielleicht spricht dies aber auch für nicht normalverteilte Daten. Relevant für den weiteren Verlauf des EpiBioManuals ist nur, dass die Variable BD_senk als annähernd normalverteilt pro Gruppe gesehen werden kann, da ihre Verteilung pro Gruppe ungefähr die Form der Normalverteilung aufweist, wie man in den Histogrammen in Abb. 10 erkennen kann.
Zusatzwissen
Tests zur Überprüfung der Normalverteilungsvoraussetzung
Es gibt auch statistische Tests, die (leider) in der Praxis genutzt werden, um schnell zu überprüfen, ob eine Normalverteilung vorliegt oder nicht. Einer davon ist der sogenannte Shapiro-Wilk-Test.
In unserem Beispiel ergibt sich ein p-Wert > 5 % pro Gruppe, sodass wir die Nullhypothese nicht ablehnen können (was diese Begriffe genau bedeuten, werdet ihr später im Kapitel statistische Tests noch genauer erfahren), was nach Interpretation des Tests dafür spricht, dass die vorliegenden Daten der Variablen BD_senk annähernd normalverteilt sind.
ABER: Wir möchten euch an dieser Stelle von der Nutzung solcher Tests abraten und die grafische Überprüfung der Normalverteilungsvoraussetzung empfehlen. Warum? Problematisch an diesen Tests ist ihre starke Abhängigkeit von der Stichprobengröße: Bei sehr kleinen Stichproben kommt es schnell zu nicht signifikanten Ergebnisse, sodass fälschlicherweise auf eine annähernde Normalverteilung geschlossen wird. Bei sehr großen Stichproben hingegen werden selbst kleinste Abweichungen von der Normalverteilung signifikant und damit die Normalverteilungsvoraussetzung als nicht erfüllt eingestuft. Außerdem werden wir später noch auf das Multiplizitätsproblem zu sprechen kommen.
Transformationen
In der Praxis sind leider nicht alle metrischen Variablen automatisch normalverteilt, was aber für viele statistische Tests eine zwingende Voraussetzung ist. Deshalb gibt es bestimmte Transformationen, die versuchen, eine nicht normalverteilte Variable in eine normalverteilte Variable umzuwandeln.
Stellt man z. B. ein Histogramm der Daten auf und kann so sehen, dass die Verteilung eben nicht symmetrisch um den Mittelwert verteilt ist, sondern mehr Masse auf der linken (linkssteil, rechtsschief) Seite liegt, handelt es sich nicht um eine normalverteilte Variable. Es kann mithilfe einer logarithmischen Transformation Y = \ln(X) versucht werden, normalverteilte Daten zu erhalten, die für die weitere Analyse oft vorteilhaft sind. Es gibt auch noch andere Transformationen, die genutzt werden, wenn die Verteilung einer Zufallsvariable eine andere Form (z. B. linksschief) aufweist. Auf diese wird an dieser Stelle aber nicht weiter eingegangen.
t-Verteilung
Die t-Verteilung oder auch Student-t-Verteilung wurde 1908 von William Sealy Gosset unter seinem Pseudonym „Student“ veröffentlicht. Gosset war ein englischer Chemiker, Mathematiker und Statistiker, der übrigens nach seinem Studium in der Guinness-Brauerei zu arbeiten begann und dort sein statistisches Wissen zur Optimierung des Brauprozesses praktisch anwenden konnte.2Siehe dazu Gossets Biografie.
Die t-Verteilung weist ähnliche Eigenschaften auf wie die Standardnormalverteilung: Sie ist glockenförmig, eingipflig und symmetrisch um die Null verteilt. Statt der tatsächlichen, in der Praxis oft unbekannten Standardabweichung ist die t-Verteilung im Gegensatz zur Normalverteilung durch die empirische Standardabweichung bestimmt. Diese lässt sich mithilfe der Anzahl der Freiheitsgrade df berechnen, die maßgeblich von der Stichprobengröße abhängt. Die Freiheitsgrade sind die Anzahl frei zu wählender Parameter. Im Falle des t-Tests für unabhängige Stichproben, den wir euch beibringen, beträgt die Anzahl der Freiheitsgrade df=n-2 , wobei n die Stichprobengröße angibt. In Abbildung 11 sind mehrere t-Verteilungen für unterschiedliche Freiheitsgrade abgebildet.

Es wird deutlich, dass sie für kleine Werte von df einen flacheren Verlauf als die Standardnormalverteilung hat (da ihre Standardabweichung dann größer als 1 ist) und sich bei größeren Werten von df immer weiter an die Standardnormalverteilung mit einer Standardabweichung von 1 annähert. Die t-Verteilung wird beispielsweise beim später erläuterten t-Test angewendet, wo sich der kritische Wert als Quantil der t-Verteilung für eine bestimmte Anzahl an Freiheitsgraden ergibt. Um diese Quantile zu ermitteln, bieten sich sogenannte Verteilungstabellen an. Schau dir die Tabelle der t-Verteilung an, in der sich die kritischen Werte für ein bestimmtes Signifikanzniveau \alpha (Achtung: es wird zwischen einseitigen und zweiseitigen Tests unterschieden, sodass für unseren Fall nur die zweite Zeile relevant ist) und eine bestimmte Anzahl an Freiheitsgraden (hier durch n bezeichnet) ablesen lassen.
Chi-Quadrat-Verteilung
Die Chi-Quadrat-Verteilung (Abb. 12) ist im Gegensatz zur Normalverteilung nicht symmetrisch um den Nullpunkt verteilt, sondern ist mit mehr Masse auf der linken Seite der Verteilung rechtsschief/linkssteil und nimmt nur positive Werte an.

Ihre spezifische Form ist abhängig von der Anzahl an Freiheitsgraden df. Wir werden die Chi-Quadrat-Verteilung vor allem bei Kreuztabellen anwenden. Hier ergibt sich die Anzahl der Freiheitsgrade aus der Anzahl an Ausprägungen der Variablen. Bei der Kreuztabelle einer Variablen x mit 3 Ausprägungen und einer Variablen y mit 4 Ausprägungen berechnet sich die Anzahl der Freiheitsgrade beispielsweise zu df=(4-1)∙(3-1)=6. Für den einfachsten Fall zweier dichotomer Variablen ergibt sich die Anzahl an Freiheitsgraden wie folgt: df=(2-1)∙(2-1)=1. Auch diese Verteilung nähert sich bei wachsender Anzahl an Freiheitsgraden immer mehr der Form einer Normalverteilung an. In ihrer einfachsten Form, also mit einem Freiheitsgrad df=1, charakterisiert sie die Verteilung des Quadrats einer standardnormalverteilten Zufallsvariable. Durch das Quadrieren ergeben sich also die ausschließlich positiven Werte der Verteilung und ihr Name. Die Quantile der Chi-Quadrat-Verteilung finden z. B. bei der Durchführung des später thematisierten Chi-Quadrat-Tests Anwendung. Wie bereits erwähnt, können wir diese Quantile mithilfe einer Verteilungstabelle ermitteln. Schaue dir die Tabelle der Chi-Quadrat-Verteilung an, in der sich die kritischen Werte für ein bestimmtes Signifikanzniveau \alpha und eine bestimmte Anzahl an Freiheitsgraden (hier durch n bezeichnet) ablesen lassen.
LITERATURVERZEICHNIS
Die Inhalte dieses Abschnitts sind angelehnt an:
Zusammenfassung
In der nachfolgenden Tabelle werden alle in diesem Abschnitt erläuterten Kenngrößen und grafischen Darstellungen zusammengefasst, die für die Beschreibung einer spezifisch skalierten Variablen geeignet sind.
| Skalenniveau | Maßzahlen | Tabelle / Grafik |
|---|---|---|
| Nominal | Häufigkeitstabellen Balkendiagramm | |
| Ordinal | Absolute Häufigkeit Relative Häufigkeit Minimum, Maximum Quantile, Quartile Median Interquartilsabstand (IQR) | Häufigkeitstabellen Balkendiagramm Boxplot |
| Metrisch | Minimum, Maximum Quantile, Quartile Median Interquartilsabstand (IQR) Mittelwert Varianz, Standardabweichung | Boxplot Histogramm |
| Ereigniszeit | Mediane Ereigniszeit Personen unter Risiko Kaplan-Meier-Schätzer | Kaplan-Meier-Kurve |
Fußnoten
- 1Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2023), Universitätsklinikum Hamburg-Eppendorf.
- 2Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2023), Universitätsklinikum Hamburg-Eppendorf.
- 3Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2023), Universitätsklinikum Hamburg-Eppendorf.
- 4Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2023), Universitätsklinikum Hamburg-Eppendorf.
- 5Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2023), Universitätsklinikum Hamburg-Eppendorf.
- 6Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2023), Universitätsklinikum Hamburg-Eppendorf, angelehnt an Abb. 2 auf S. 73 in Schumacher, Martin; Olschewski, Manfred (2008): Analyse von Ereigniszeiten – Teil I. In: Methodik klinischer Studien. Methodische Grundlagen der Planung, Durchführung und Auswertung. Martin Schumacher, Gabi Schulgen (Hrg.), 3. Aufl., Springer Verlag, Kapitel 5.
- 7Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2023), Universitätsklinikum Hamburg-Eppendorf.
- 8Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2023), Universitätsklinikum Hamburg-Eppendorf.
- 9Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2023), Universitätsklinikum Hamburg-Eppendorf.
- 10Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2023), Universitätsklinikum Hamburg-Eppendorf.
- 11Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2023), Universitätsklinikum Hamburg-Eppendorf.
- 12Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2023), Universitätsklinikum Hamburg-Eppendorf.

