Korrelation und Regression

Studienauswertung

Sowohl Korrelation als auch die lineare Einfach-Regression betrachten den Zusammenhang zwischen zwei metrischen Variablen. Deshalb werden sie in diesem Abschnitt gemeinsam erklärt.

Soll die Stärke des Zusammenhangs zwischen zwei metrischen Variablen quantifiziert werden, kommt die Korrelation ins Spiel. Welche Variable dabei Einfluss auf die andere hat, also die Richtung des Zusammenhangs, wird durch die Korrelation nicht untersucht.

Um sich einen ersten Eindruck über eine eventuelle Korrelation zu verschaffen, kann ein Streudiagramm verwendet werden, wie im Beispiel veranschaulicht wird.

Beispiel "Blutdrucksenker"

Wir betrachten das Streudiagramm zweier metrischer Variablen unseres Beispiels (Abb. 1): Auf der $x$ -Achse wird der BMI, eine neu erstellte Variable als Zusammenhang zwischen Körpergröße in cm und Gewicht in kg, betrachtet. Die $y$ -Achse gibt die Senkung des systolischen Blutdrucks nach 5 Wochen in mmHg an.
Es wird an dieser Stelle nicht mehr zwischen Interventions- und Kontrollgruppe unterschieden, sondern der Zusammenhang zwischen BMI und Blutdrucksenkungen in der Gesamtstichprobe untersucht.

Da wir sehen, dass höhere Werte des BMI auf der $x$ -Achse tendenziell mit niedrigeren Werten der Blutdrucksenkung auf der $y$ -Achse einhergehen, spricht das Streudiagramm für eine negative Korrelation zwischen den beiden Variablen. Dies sieht man auch anhand der negativen Steigung der eingezeichneten Gerade, die die bestmögliche lineare Annäherung an unsere Daten angibt (die später thematisierte Regressionsgerade).

Ein Streudiagramm kann außerdem hilfreich sein, um Ausreißer in den Daten, also Datenpunkte, die nicht im gängigen Wertebereich der betrachteten Variablen liegen, zu identifizieren. Ein möglicher Ausreißer ist in der Grafik in rot markiert und mit der zugehörigen ID 64 beschriftet, um einfacher noch einmal zu prüfen, dass kein Fehler in diesem Datensatz vorliegt. In diesem Fall handelt es sich um einen Wert, der zwar auffällig und somit ein Ausreißer, aber dennoch biologisch möglich ist. Nach erneuter Prüfung wurde er als korrekter Datenpunkt beurteilt und wird somit nicht aus der weiteren Analyse entfernt.

Der Pearson-Korrelationskoeffizient ist die gängigste Kenngröße, um eine Korrelation zwischen zwei Variablen zu quantifizieren. Er wird wie folgt berechnet:

$r_{xy} = \frac{\text{Cov}(x,y)}{SD(x) \cdot SD(y)} = \frac{\frac{1}{n-1} \cdot \sum_{i=1}^{n}(x_i – \overline{x}) \cdot (y_i – \overline{y})}{\sqrt{\frac{1}{n-1} \cdot \sum_{i=1}^{n}(x_i – \overline{x})^2} \sqrt{\frac{1}{n-1} \cdot \sum_{i=1}^{n}(y_i – \overline{y})^2}}.$

Der Ausdruck im Zähler des Pearson-Korrelationskoeffizenten ist die sogenannte Kovarianz $\text{Cov}(x,y)$ . Sie beschreibt, wie zwei Variablen $x$ und $y$ zusammen variieren, kann aber wie die Varianz nicht sinnvoll interpretiert werden. Erst durch die Standardisierung mithilfe der Standardabweichungen, sodass sich der Pearson-Korrelationskoeffizient ergibt, kann die Interpretation erfolgen.

Beispiel "Blutdrucksenker"

In unserem Beispiel ergibt sich für den Korrelationskoeffizienten zwischen BMI und der Blutdrucksenkung das folgende Ergebnis:

$r_{xy} = \frac{\text{Cov}(x,y)}{SD(x) \cdot SD(y)} \approx \frac{-17,34}{6.50 \cdot 7,34} \approx -0,36$

Die Werte für die Standardabweichungen und Kovarianz der Variablen wurden an dieser Stelle von Statistiksoftware für unsere Daten berechnet.

Der Pearson-Korrelationskoeffizient kann Werte zwischen $-1$ und $+1$ annehmen. Ein negativer Wert bedeutet, dass höhere Werte der einen Variablen mit niedrigeren Werten der anderen einhergehen (und andersherum). Ein positiver Korrelationskoeffizient bedeutet, dass beide Variablen gemeinsam in eine Richtung variieren. Die drei Extremfälle (perfekte positive Korrelation, perfekte negative Korrelation und keine Korrelation) und zwei recht eindeutige Fälle von positiver und negativer Korrelation sind in den folgenden Streudiagrammen (Abb. 2) abgebildet.

Man sieht, dass im Falle einer perfekten Korrelation mit $r\approx \pm 1$ die Punkte auf einer steigenden bzw. fallenden Gerade liegen. Existiert keine Korrelation mit $r\approx 0$ , befinden sich die Datenpunkte in einer zufälligen Punktwolke ohne bestimmte Form. Auch ein nichtlinearer Zusammenhang zwischen den Variablen, wie im Streudiagramm unten rechts dargestellt, kann mithilfe des Streudiagramms festgestellt werden. In diesem Fall stellt der Pearson-Korrelationskoeffizient kein sinnvolles Maß für die Korrelation zweier Variablen dar.

Beispiel "Blutdrucksenker"

Wir sprechen in unserem Beispiel mit $r_{xy}\approx -0,36$ von einer moderaten negativen Korrelation zwischen den Variablen BMI und systolischer Blutdrucksenkung nach 5 Wochen in mmHg.

ACHTUNG: Es ist grundsätzlich sehr wichtig, dass ihr Korrelation nicht mit Kausalität verwechselt. Darauf wird im Abschnitt Confounding, Bias & Co. noch genauer eingegangen.

In diesem Abschnitt liegt der Fokus auf der linearen Einfach-Regression: Es wird auf die Methode der kleinsten Quadrate zur Schätzung der Regressionsgeraden und das Bestimmtheitsmaß zur Beurteilung der Güte des Regressionsmodells eingegangen.

Außerdem werden kurz die multiple lineare Regression und weitere komplexere Regressionsmodelle thematisiert.

Lineare Einfach-Regression

Die lineare Einfach-Regression versucht auf Basis der Korrelation zwischen zwei Variablen, einen linearen Zusammenhang zwischen diesen zu modellieren und so genauer zu beschreiben. Im Gegensatz zur Korrelationsanalyse ist es hier relevant, welche Variable als Einflussvariable (im Kontext der Regressionsanalyse meist als unabhängige Variable $x$ bezeichnet) und welche als Outcome (abhängige Variable $y$ ) gesehen wird. Dies sollte aufgrund inhaltlicher, sachlogischer Überlegungen vor Analysebeginn festgelegt werden.

Für die lineare Einfach-Regression ist es notwendig, dass es sich bei $y$ um eine metrische Variable handelt. Die Variable $x$ kann grundsätzlich auch kategorial sein, aber im Rahmen dieser Vorlesung wird auch hier nur eine metrische Variable betrachtet.

Download der Abb. 3 in Listenform als PDF

Mithilfe der im Rahmen der Analyse hergeleiteten Regressionsgleichung können auf Basis der Werte der unabhängigen Variable Vorhersagen über die abhängige Variable gemacht werden.

Wir schauen uns nun an, wie die Regressionsgleichung in Form einer Gerade abgeleitet wird. Im ersten Schritt sollte, z. B. mithilfe eines Streudiagramms wie im Abschnitt zur Korrelation abgebildet, sichergestellt werden, dass der zugrundeliegende Zusammenhang zwischen der unabhängigen und der abhängigen Variablen annähernd linear ist und sich so hinreichend gut durch eine Gerade beschreiben lässt (ansonsten siehe komplexere Regressionsmodelle).
Eine Gerade wird durch die folgende Gleichung beschrieben

$y=a+b\cdot x$

Dabei beschreibt $a$ den Punkt auf der $y$ -Achse, wo die Gerade die $y$ -Achse schneidet (Achsenabschnitt) und $b$ die Steigung der Geraden (Steigungsparameter) – vielleicht kommt euch das aus der Schule noch bekannt vor.

Beispiel "Blutdrucksenker"

Wir wollen uns für unser Beispiel erneut den linearen Zusammenhang zwischen dem BMI und der Blutdrucksenkung nach 5 Wochen in mmHg ( $BD\_senk$ ) in der gesamten Stichprobe anschauen.

Die folgende Gerade, die diesen Zusammenhang annähert, soll auf Basis der Stichprobendaten geschätzt werden:

$BD\_senk=a+b \cdot BMI.$

Die Koeffizienten $a$ und $b$ müssen nun so geschätzt werden, dass die resultierende Gerade die Punktwolke der Stichprobe möglichst gut beschreibt. Das wird mithilfe der sogenannten Methode der kleinsten Quadrate erreicht.

Zusatzwissen

Methode der kleinsten Quadrate

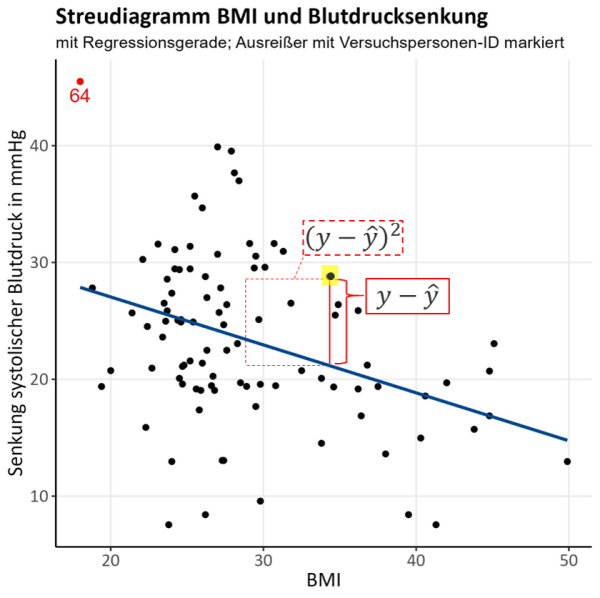
Das Ziel der Methode ist es, die Regressionsgerade zu finden, die die Daten der Stichprobe am besten beschreibt. Am naheliegendsten wäre es, einfach die Abweichungen von jedem einzelnen Datenpunkt zur Regressionsgerade zu betrachten, wie in Abb. 4 für einen in gelb markierten Beispieldatenpunkt eingezeichnet. Die Abweichung zwischen dem tatsächlichen Wert und dem geschätzten Wert durch die Regressionsgerade wird auch als Residuum (rot-durchgezogene Linie) bezeichnet. Würde man die Summe all dieser Residuen minimieren, würde sich so ganz leicht die beste Regressionsgerade finden – oder? Ganz so einfach ist es leider nicht. Da die Abweichungen zur Geraden teilweise positive und teilweise negative Werte annehmen, würden sie sich beim Aufsummieren gegenseitig aufheben. Aus diesem Grund werden die quadrierten Abweichungen von der Regressionsgerade (rot-gestrichelte Linie in Abb. 4) betrachtet. Durch das Quadrieren ergeben sich nur noch positive Werte („Minus mal Minus ergibt Plus“), die sich nicht mehr gegenseitig aufheben können. Es werden nun also die Quadrate der Residuen minimiert (der Flächeninhalt eines Quadrats berechnet sich nämlich genau durch das Quadrieren der Seitenlänge). Daher ergibt sich auch der Name „Methode der kleinsten Quadrate“.

Aus dem Minimierungsproblem

$\sum_{i=1}^{n} (y_i – \hat{y}_i)^2 \rightarrow \min!$

ergeben sich durch Ableiten und Nullsetzen die unten genannten Formeln für die Schätzung der Regessionskoeffizienten. Wenn du dir die Herleitung der Regressionskoeffizienten noch genauer anschauen möchtest, dann schaue dir das PDF von Weiß 2013, S. 310 f. an.

Aus der KQ-Methode ergeben sich die folgenden Formeln, um die Regressionskoeffizienten auf Basis der Stichprobendaten zu schätzen

$\hat{b} = \frac{\text{Cov}(x, y)}{\text{Var}(x)}$

$\hat{a} = \bar{y} – \hat{b} \cdot \bar{x}$

Durch das „Dach“ auf dem Koeffizienten wird deutlich gemacht, dass es sich um Schätzungen auf Basis der Stichprobe handelt. Es werden für die Berechnung der Schätzer also die Stichprobenmittelwerte beider Variablen, die empirische Varianz der unabhängigen Variablen $\text{Var}(x)$ und die Kovarianz beider Variablen $\text{Cov}(x, y)$ , die bereits im letzten Abschnitt zum Korrelationskoeffizienten thematisiert wurde, benötigt.

Mithilfe der geschätzten Regressionskoeffizienten und mit den Werten der unabhängigen Variablen $x$ aus unserer Stichprobe können wir nun auf Basis der Regressionsgeraden

$\hat{y} = \hat{a} + \hat{b} \cdot x$

Schätzungen für die abhängige Variable $\hat{y}$ berechnen. Es ist außerdem möglich ganz neue Werte für $x$ einzusetzen, die noch nicht in der Stichprobe vorkamen und dann Prognosen für $\hat{y}$ zu machen. Die einzige Bedingung ist, dass die für $x$ eingesetzten Werte nicht über den beobachteten Wertebereich hinausgehen (es sollten also kein Werte eingesetzt werden, die kleiner als das Minimum von $x$ bzw. größer als das Maximum von $x$ sind). Eine sogenannte Extrapolation ist deshalb problematisch, weil wir uns nicht sicher sein können, ob die geschätzte Regressionsgerade auch außerhalb unseres Beobachtungsbereichs die beste Annäherung an die realen Datenpunkte ist oder ob diese sich dort anders verteilen.

Beispiel "Blutdrucksenker"

Wir schätzen nun die Regressionskoeffizienten für unser Beispiel:

$\hat{b} = \frac{\text{Cov}(x, y)}{\text{Var}(x)} \approx \frac{-17,34}{(6,50)^2} \approx -0,41$

$\hat{a} = \bar{y} – \hat{b} \cdot \bar{x} \approx 23,35 – (-0,41) \cdot 29,00 \approx 35,24$

Damit ergibt sich die Regressionsgerade

$\widehat{BD\_senk} = 35,24 – 0,41 \cdot BMI.$

Setzen wir beispielsweise einen BMI von 26 ein (Durschnitt in Deutschland), ergibt sich nach 5 Wochen eine geschätzte Blutdrucksenkung von 24,58 mmHg.

Der geschätzte Wert der Blutdrucksenkung für einen BMI von 53 sollte nicht als geeignete Prognose gesehen werden, da wir in unseren Daten nur Versuchspersonen mit einem BMI bis zu 50 betrachten und es sich somit um Extrapolation handeln würde.

Wir wollen uns nun noch einmal genauer anschauen, wie wir die Regressionskoeffizienten $\hat{a}$ und $\hat{b}$ interpretieren können.

Der Koeffizient $\hat{a}$ gibt den geschätzten Wert $\hat{y}$ an, wenn man für $x$ den Wert Null einsetzen würde (denn dann würde der zweite Summand der Geradengleichung wegfallen und es bleibt nur noch $\hat{y}=\hat{a}$ übrig).

Der Koeffizient $\hat{b}$ sagt aus, wie sich die abhängige Variable $y$ verändert, wenn die unabhängige Variable $x$ um genau eine Einheit vergrößert wird (Stichwort aus der Schule: Steigungsdreieck).

Beispiel "Blutdrucksenker"

In unserem Beispiel ergibt die Interpretation von $\hat{a}$ wenig Sinn, da dieser die Blutdrucksenkung bei einem $BMI = 0$ beschreiben würde, was in der Praxis nicht existiert. An dieser Stelle wäre es vielleicht besser, die Daten so zu transformieren, dass die Werte des BMIs immer die Abweichung zum durchschnittlichen BMI in der Stichprobe oder in Deutschland angeben (sogenannte z-Transformation). Damit würde der Koeffizient $\hat{a}$ die Blutdrucksenkung bei durchschnittlichen BMI (denn hier ist die Abweichung gleich Null) angeben.

Der Koeffizient $\hat{b}$ wird wie folgt interpretiert: Steigt der BMI um eine Einheit, dann sinkt die Blutdrucksenkung im Durchschnitt um 0,41 mmHg – d. h. also mit steigendem BMI nimmt die Blutdrucksenkung ab (wie auch im Abschnitt Korrelation berichtet).

Gütemaß der linearen Regression

Ein Maß für die Güte der Vorhersage der Variable $y$ durch die Variable $x$ ist das sogenannte Bestimmtheitsmaß $r^2$ , das sich bei der linearen Einfach-Regression durch Quadrieren des Korrelationskoeffizienten $r$ zwischen den zwei betrachteten Variablen ergibt. Das Bestimmtheitsmaß $r^2$ ist somit wie der Korrelationskoeffizient $r$ ein Maß für die Stärke des Zusammenhangs zwischen $x$ und $y$ .

Die Werte von $r^2$ liegen zwischen 0 und 1 und geben an, wie viel Prozent der Gesamtstreuung in $y$ durch die Streuung in $x$ erklärt werden kann. Ist dieser Wert hoch (welcher Wert als hoch angesehen wird, hängt von Fragstellung/Fachgebiet/Betrachter ab), spricht das dafür, dass die Regressionsgleichung gut für Prognosen von $y$ geeignet ist, da ein starker linearer Zusammenhang zwischen beiden Variablen besteht.

Beispiel "Blutdrucksenker"

In unserem Beispiel ergibt sich $r^2=0,13$ . Das heißt lediglich 13 % der Gesamtstreuung in der Blutdrucksenkung kann durch den BMI erklärt werden. Da es sich um einen relativ geringen Wert handelt, können wir davon ausgehen, dass es bessere Modelle gibt (z. B. mit mehr berücksichtigten Variablen, siehe Abschnitt Komplexere Regressionsmodelle), um die Variable BD_senk zu modellieren.

Die Ergebnisse sind in der folgenden Grafik (Abb. 5) noch einmal zusammengefasst:

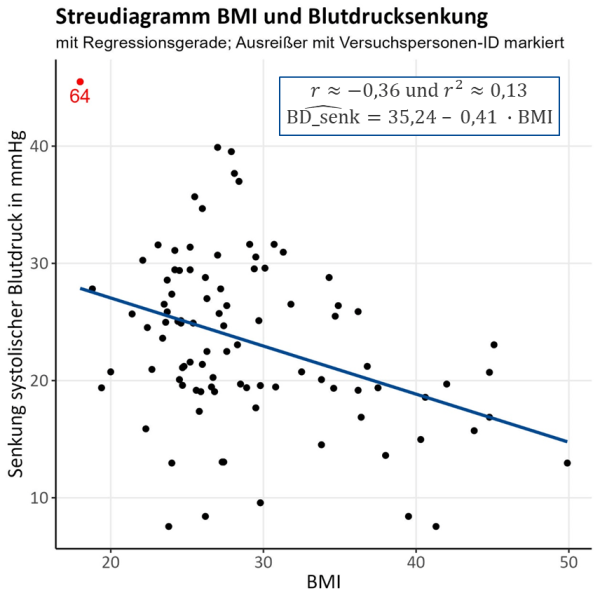
ACHTUNG: Es ist zu beachten, dass Ausreißer die Regressionsgerade maßgeblich in eine Richtung verzerren können. Manchmal ist es dann sinnvoll, diese aus der Analyse auszuschließen. Dies soll an dieser Stelle aber nicht weiter thematisiert werden.

Multiple lineare Regression

Nicht immer genügt es, einen linearen Zusammenhang zwischen zwei Variablen zu betrachten, um den tatsächlichen Zusammenhang realistisch zu modellieren. Die multiple lineare Regression wird genutzt, wenn nicht nur eine unabhängige Variable von Interesse ist, sondern der simultane Einfluss mehrerer Variablen auf die abhängige Variable und auch Interaktionen dieser untereinander betrachtet werden sollen.

In das multiple Regressionsmodell können außerdem noch weitere Variablen aufgenommen werden, die zwar nicht im eigentlichen Fokus der Analyse stehen, aber trotzdem Einfluss auf die abhängige Variable haben könnten. Die Aufnahme sogenannter Kovariablen ist sinnvoll, um Confounding zu vermeiden, was im Abschnitt Confounding, Bias & Co. genauer thematisiert wird.

Beispiel "Blutdrucksenker"

Wir haben für unser Beispiel ein multiples lineares Regressionsmodell aufgestellt, das den folgenden Zusammenhang beschreibt: Welchen Einfluss haben die Variablen Gruppenzuteilung, Baselinewert der Blutdruckmessung in mmHg, BMI, sportliche Aktivität und Alter auf die Variable der Blutdrucksenkung nach 5 Wochen in mmHg?

Unser Modell, liefert die folgenden Ergebnisse (wir betrachten hier lediglich die inhaltliche Interpretation):
Die Blutdrucksenkung nach 5 Wochen in mmHg wird unter gleichzeitiger Berücksichtigung der jeweils anderen Variablen größer bei …

… Zuteilung zur Interventionsgruppe (statt zur Kontrollgruppe).
… steigendem Baselinewert der Blutdruckmessung in mmHg.
… sinkendem BMI.
… sinkender sportlicher Aktivität.
… sinkendem Alter (wobei es sich hierbei nicht um einen signifikanten Effekt handelt).
… Männern im Vergleich zu Frauen (wobei es sich hierbei erneut nicht um einen signifikanten Effekt handelt).

Das Bestimmtheitsmaß $r^2$ steigt in diesem Modell auf 58 %, was einen deutlich höheren Erklärungsgehalt zeigt als das oben aufgestellte einfache lineare Regressionsmodell.

Komplexere Regressionsmodelle

Es gibt außerdem noch zahlreiche „Erweiterungen“ bzw. Abwandlungen der linearen Regression, um auch komplexere Sachverhalte modellieren zu können.

Es ist in der Praxis nicht immer der Fall, dass die betrachtete abhängige Variable metrisch ist. Handelt es sich z. B. um eine dichotome abhängige Variable, ist eine logistische Regression die gängigste Alternative zur linearen Regression. Für ordinal verteile Outcomes kommt das sogenannte kumulative Logit-Regressionsmodell in Frage und für die Analyse von Outcomes auf der Ereigniszeitskala die Cox-Regression.

Außerdem gibt es auch die sogenannte nichtlineare Regression, um Zusammenhänge zwischen den betrachteten Variablen zu analysieren, die nicht durch eine Gerade zu approximieren sind. Anstelle der Regressionsgleichung in Form einer Gerade, wird dann eine nichtlineare Funktion betrachtet (z. B. die Exponentialfunktion).

Wie genau die genannten Verfahren durchzuführen sind, wird hier nicht weiter thematisiert, da dies den Rahmen dieser Veranstaltung sprengen würde. Es ist aber sinnvoll, dass ihr einmal die Namen der Methoden gehört habt, um beim Lesen wissenschaftlicher Studien grob zu verstehen, warum welche Methode angewandt wurde. Das am besten geeignete Analyseverfahren zu finden, bedarf teilweise einer hohen Fachkenntnis über die theoretischen Hintergründe der Fragestellung.

LITERATURVERZEICHNIS

Die Inhalte dieser Seite sind angelehnt an:

Weiß, Christel (2013): Beschreibung eines Zusammenhangs. In: Christel Weiß (Hg.): Basiswissen Medizinische Statistik. Mit 20 Tabellen. 6., überarbeitete Auflage. Berlin, Heidelberg: Springer (Springer-Lehrbuch), S. 73-89, Kapitel 5.2 und 5.3.

Fußnoten

1
Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2023), Universitätsklinikum Hamburg-Eppendorf.
2
Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2023), Universitätsklinikum Hamburg-Eppendorf.
3
Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2023), Universitätsklinikum Hamburg-Eppendorf.
4
Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2023), Universitätsklinikum Hamburg-Eppendorf.
5
Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2023), Universitätsklinikum Hamburg-Eppendorf.