Grundgesamtheit und Stichprobe
Studienplanung
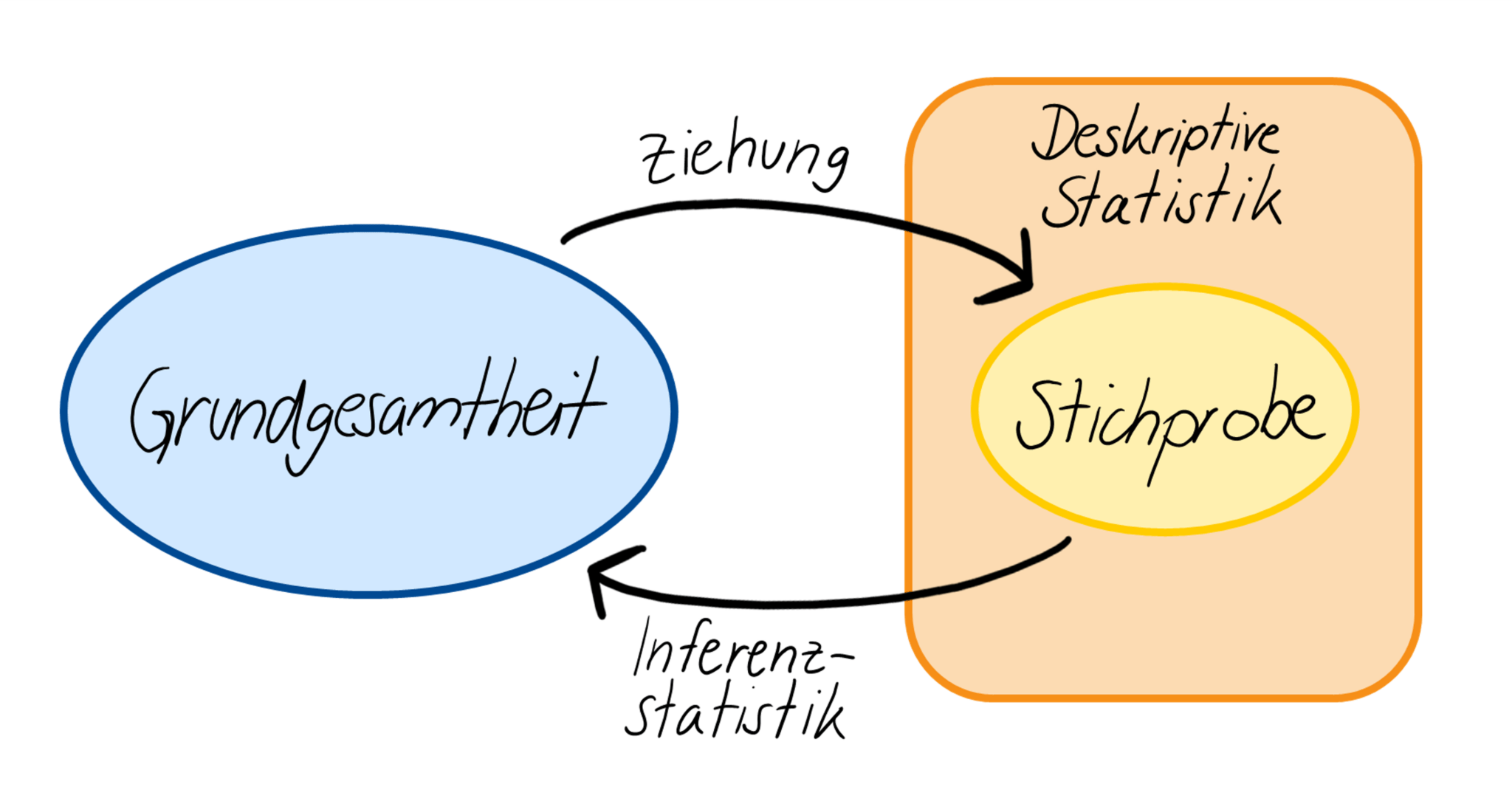
Studien (fast) jeder Art sind an einer bestimmten Personengruppe interessiert. Um Aussagen über diese Personengruppe, die sogenannte Grundgesamtheit, treffen zu können, müssten theoretisch alle Personen dieser Gruppe in der Untersuchung berücksichtigt werden, was in der Praxis aber eigentlich nie möglich ist. Zur Lösung dieses Problems wird für die Durchführung einer Studie eine Stichprobe aus der Grundgesamtheit gezogen. Eine Stichprobe ist somit eine hinreichend große Auswahl von Personen aus der entsprechenden Grundgesamtheit. Was genau bedeutet nun aber hinreichend groß? Um diese Frage zu beantworten, kommt die sogenannte Fallzahlplanung ins Spiel. Ist die Stichprobe zu klein, steigt die Wahrscheinlichkeit für falsche Schlussfolgerungen und die Wahrscheinlichkeit, dass die Ergebnisse unserer Studie nur durch Zufall entstanden sind und bei einer Wiederholung des Experiments ganz anders aussehen würden. Eine zu große Stichprobe bringt auch it sich: Einerseits geht sie mit höheren Kosten und höherem Aufwand als nötig einher. Auch aus ethischen Gründen kann eine große Stichprobe nachteilig sein, wenn z. B. unnötig viele Patient:innen einem Risiko ausgesetzt werden oder die Therapie verspätet auf den Markt kommt. Außerdem werden durch eine zu große Stichprobe schon bereits kleinste Effekte als signifikant eingestuft, die in der Realität vielleicht gar keine medizinische Relevanz aufweisen würden. Die Fallzahlplanung hat also das Ziel anhand von detailliertem medizinischen Fachwissen und auf Basis statistischer Überlegungen die optimale Stichprobengröße zu ermitteln. Im Kapitel Statistische Tests wird später noch auf die Details der Fallzahlplanung eingegangen. Zum jetzigen Zeitpunkt genügt es, ihr grundlegendes Konzept zu verstehen.
Die gezogene Stichprobe sollte nicht nur hinreichend groß, sondern auch möglichst repräsentativ sein, also die Eigenschaften der anvisierten Grundgesamtheit widerspiegeln. Das große Ziel ist es, auf Basis dieser repräsentativen Stichprobe (siehe Repräsentativität) mithilfe statistischer Methoden Aussagen über die Grundgesamtheit zu treffen (siehe Inferenzstatistik).
Um die Grundgesamtheit treffend widerzuspiegeln, benötigt es die sogenannten Einschlusskriterien, welche Eigenschaften, wie z. B. das Alter oder das Geschlecht der Studienpopulation, festlegen. Diese können je nach Anforderung weit oder eng formuliert werden, sollten aber stets eine sinnvolle und erreichbare Population abbilden. Den Einschlusskriterien stehen die Ausschlusskriterien gegenüber. Sie legen fest, welche Eigenschaften die Studienteilnahme einer Person unterbinden würden (ein übliches Kriterium sind beispielsweise Schwangerschaften). Sinnvolle Ein- und Ausschlusskriterien festzulegen, ist eine der wichtigsten Maßnahmen, um die Repräsentativität der Stichprobe zu erreichen.
Des Weiteren sollte zur Erreichung von Repräsentativität eine zufällige Stichprobenziehung erfolgen. Das bedeutet, dass jedes Mitglied der Grundgesamtheit mit gleicher Wahrscheinlichkeit in die Stichprobe gezogen wird.
Beispiel "Blutdrucksenker"
In unserem Beispiel soll, wie gesagt, eine kontrollierte Studie zur Wirkung eines Blutdruck senkenden Medikaments in der erwachsenen Bevölkerung mit einem zu behandelnden Bluthochdruck durchgeführt werden, in der die neue Intervention mit der Standardtherapie verglichen wird. Die Grundgesamtheit „erwachsene Bevölkerung mit einem zu behandelnden Bluthochdruck“ muss nun genauer definiert werden, um eine entsprechende Stichprobe zur Ermöglichung der Studie zu ziehen. Es werden Personen mit einem systolischen Blutdruck ab 140 mmHg in die Studie eingeschlossen. Außerdem könnte für die Definition der „erwachsenen Bevölkerung“ das Alter zwischen 18 und 59 Jahren ein Kriterium sein. Die Stichprobe sollte entsprechend keine Personen unter 18 Jahren und über 59 Jahren beinhalten, da sie sonst nicht mehr die anvisierte Grundgesamtheit widerspiegelt. Des Weiteren werden Schwangere und Patient:innen mit einem Körpergewicht unter 45 kg oder einem BMI kleiner als 18 kg/m2 oder größer als 50 kg/m2 aus der Stichprobe ausgeschlossen, da ein höheres Risiko für Nebenwirkungen befürchtet wird.
Die Fallzahlplanung beruht in unserem Beispiel auf medizinischem Fachwissen der beteiligten Forscher:innen, die zum Beispiel den erwarteten Unterschied zwischen beiden Therapien quantifizieren. Es wird eine Stichprobengröße von 100 Proband:innen berechnet, die eingeschlossen werden sollen.
Parameter vs. Schätzer
Parameter und Schätzer sind die statistischen Kenngrößen, die an die Grundgesamtheit bzw. die Stichprobe gebunden sind und werden deshalb an dieser Stelle erläutert.
(Wahre) Parameter sind die wahren Werte einer Bevölkerung bzw. der Grundgesamtheit und (empirische) Schätzer die Möglichkeiten sich mittels einer Stichprobe an diese Parameter anzunähern. Parameter können in der Regel nicht erfasst werden, da wir von allen Personen oder Objekten Informationen benötigen würden, die der Grundgesamtheit angehören.
Deshalb benötigen wir Schätzer: Schätzer erlauben es, Aussagen über die Stichprobe zu tätigen und ermöglichen es damit, auf die (Parameter der) Grundgesamtheit zu schließen. Schätzer sind vielfältig und lassen sich in zwei Kategorien aufteilen: Punkt- und Streuungsschätzer. Im Abschnitt Deskriptive Kenngrößen wird im Detail auf diese eingegangen. Wir behandeln Schätzer vorerst nur als deskriptive Angaben und führen später eine weitere Kategorie von Schätzern, die Effektschätzer, ein.
Beispiel "Blutdrucksenker"
Das mittlere Alter der Patient:innen der Stichprobe \overline{x} ist z. B. ein Schätzer für das tatsächliche mittlere Alter (der Erwartungswert \mu des Alters ist hier der unbekannte gesuchte Parameter) aller Patient:innen der Grundgesamtheit.
LITERATURVERZEICHNIS
Die Inhalte dieser Seite sind angelehnt an:
Fußnoten
- 1Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2023), Universitätsklinikum Hamburg-Eppendorf.