Effektschätzer
Studienauswertung
Im letzten Abschnitt haben wir schon Punktschätzer und Streuungsschätzer kennengelernt. Eine weitere Kategorie von Schätzern sind die sogenannten Effektschätzer. Im Rahmen dieses Handbuches wollen wir uns Effektschätzer, die auf Punktschätzern basieren, genauer anschauen. Wir haben im Abschnitt zu den verschiedenen Studientypen gesehen, dass es in der medizinischen Forschung oft das Ziel ist, mehrere Gruppen von Personen hinsichtlich bestimmter Faktoren/Outcomes zu vergleichen. Dabei kommen Effektschätzer ins Spiel: Sie helfen uns, einen Unterschied zwischen diesen Gruppen (in unserem vereinfachten Fall immer zwei voneinander unabhängige Gruppen) zu quantifizieren. Wir können sie im Rahmen der Inferenzstatistik nutzen, um zu überprüfende statistische Hypothesen zu formulieren, worauf wir später genauer eingehen werden.
Wann, welcher Effektschätzer geeignet ist, hängt sowohl vom gewählten Studientyp als auch vom Skalenniveau des betrachteten primären Endpunktes (= Outcomes) ab.
Im weiteren Verlauf dieses Abschnitts sollt ihr die verschiedenen Effektschätzer kennenlernen und passend zum Studientyp und Skalenniveau auswählen können.
Zur Info:
Die Effektschätzer selbst sind, wie der Name schon sagt, Schätzungen, die auf Basis der Daten der Stichprobe geschätzt werden. Um sie als solche zu erkennen, werden sie mit einem Dach (z. B. \widehat{RD}) beschriftet. Die statistischen Hypothesen stellen hingegen Vermutungen über die anvisierte Grundgesamtheit dar. Sie werden also mithilfe der wahren Werte des vermuteten Effekts formuliert, die ohne Dach (z. B. RD) geschrieben werden.
Dichotomes Outcome
Ein dichotomes Outcome bedeutet, dass die zu untersuchende Variable genau zwei Ausprägungen aufweist. In diesem Fall ist es vom Studientyp abhängig, welcher Effektschätzer für die Aufstellung der später thematisierten statistischen Hypothesen geeignet ist.
Für experimentelle Studien (RCTs) werden Risiken betrachtet und zueinander in Verhältnis gesetzt. In einer RCT beschreibt das Risiko die relative Häufigkeit der Personen, die das definierte dichotome Outcome erfüllen, in einer der beiden Gruppen. Das Erfüllen des Outcomes (z. B. indem mit „ja“ auf die untersuchte Frage geantwortet wird) muss nicht unbedingt als etwas Negatives bewertet werden, auch wenn der Name „Risiko“ dies vielleicht suggerieren mag.
Sollen nun beide Gruppen im Zusammenhang betrachtet werden, kommen Differenzschätzer und Verhältnisschätzer ins Spiel:
Die Risikodifferenz \widehat{RD} (oder teilweise auch als Absolute Risikoreduktion bezeichnet) beschreibt, wie der Name schon vermuten lässt, die Differenz der Risiken der beiden zu vergleichenden Gruppen:
\widehat{RD} = \widehat{R_1} – \widehat{R_2}.
Sie kann Werte zwischen -1 (bzw. -100 %) und +1 (bzw. +100 %) annehmen. Das Vorzeichen bestimmt die Richtung des Zusammenhangs. Eine \widehat{RD}=0,05=5 % (bzw. \widehat{RD}=-5 %) sagt in einer RCT z. B. aus, dass die Wahrscheinlichkeit, das Outcome zu erfüllen, in Gruppe 1 um 5 Prozentpunkte größer (bzw. kleiner) ist als in Gruppe 2 (z. B. weil Gruppe 1 einem bestimmten Risikofaktor ausgesetzt ist und Gruppe 2 nicht).
Eine Alternative zur Risikodifferenz ist das Relative Risiko \widehat{RR}, das durch den Quotienten der Risiken in beiden Gruppen ermittelt wird:
\widehat{RR} = \frac{\widehat{R_1}}{\widehat{R_2}}.
Das Relative Risiko nimmt positive Werte zwischen 0 und \infty an und sagt in RCTs aus, wie viel Mal größer die Wahrscheinlichkeit, das Outcome zu erfüllen, in Gruppe 1 im Vergleich zu Gruppe 2 ist.
Ist die Risikodifferenz \widehat{RD} \approx 0 bzw. das Relative Risiko \widehat{RR} \approx 1, bedeutet das, dass kein Unterschied zwischen den betrachteten Gruppen vorliegt. Im Vergleich dazu würden \widehat{RD} = \pm 1 bzw. \widehat{RR} = 0 oder \widehat{RR} = \infty auf einen maximalen Gruppenunterschied in die jeweilige Richtung hinweisen.
Beispiel "Blutdrucksenker"
|
Empirische Daten |
Blutdruck auf < 140 mmHg gesunken | Blutdruck nicht auf < 140 mmHG gesunken | Summe |
| Neue Intervention (Intervention) | a=40 | b=6 | 46 |
| Standardtherapie (Kontrolle) | c=32 | d=17 | 49 |
| Summe | 72 | 23 | n=95 |
Auch in Kohortenstudien werden Risiken betrachtet und zueinander in Verhältnis gesetzt. Ein Risiko beschreibt in einer Kohortenstudie die Wahrscheinlichkeit, dass in einer einzelnen Gruppe über den Beobachtungszeitraum hinweg das interessierende Ereignis, z. B. die Erkrankung, eintritt. Das Risiko ist von der sogenannten (kumulativen) Inzidenz zu unterscheiden, die auch in Kohortenstudien betrachtet wird. Sie beschreibt die Neuerkrankungsrate, also die relative Häufigkeit der Personen, die innerhalb des definierten Beobachtungszeitraums erkranken, und schätzt damit das Risiko. Außerdem können aufgrund des Designs von Kohortenstudien die Inzidenzen der Exponierten mit denen der nicht Exponierten direkt verglichen werden, was in der medizinischen Forschung häufig von Interesse ist.
Wie auch in RCTs werden Differenzschätzer und Verhältnisschätzer betrachtet:
Die Risikodifferenz \widehat{RD} beschreibt auch hier die Differenz der Risiken der beiden zu vergleichenden Gruppen:
\widehat{RD} = \widehat{R_1} – \widehat{R_2}.
Sie kann auch in Kohortenstudien Werte zwischen -1 (bzw. -100 %) und +1 (bzw. +100 %) annehmen. Das Vorzeichen bestimmt die Richtung des Zusammenhangs. Eine \widehat{RD}=0,05=5 % (bzw. \widehat{RD}=-5 %) sagt z. B. aus, dass das Risiko zu erkranken in Gruppe 1 um 5 Prozentpunkte größer (bzw. kleiner) ist als in Gruppe 2 (z. B. weil Gruppe 1 einem bestimmten Risikofaktor ausgesetzt ist und Gruppe 2 nicht).
Eine Alternative zur Risikodifferenz ist auch in Kohortenstudien das Relative Risiko \widehat{RR}, das durch den Quotienten der Risiken in beiden Gruppen ermittelt wird:
\widehat{RR} = \frac{\widehat{R_1}}{\widehat{R_2}}.
Das Relative Risiko nimmt positive Werte zwischen 0 und \infty an und sagt in einer Kohortenstudie aus, wie viel Mal größer das Erkrankungsrisiko in Gruppe 1 im Vergleich zu Gruppe 2 ist.
Ist die Risikodifferenz \widehat{RD} \approx 0 bzw. das Relative Risiko \widehat{RR} \approx 1, bedeutet das, dass kein Unterschied zwischen den betrachteten Gruppen vorliegt. Im Vergleich dazu würden \widehat{RD} = \pm 1 bzw. \widehat{RR} = 0 oder \widehat{RR} = \infty auf einen maximalen Gruppenunterschied in die jeweilige Richtung hinweisen.
Beispiel: Kohortenstudie
Eine Meta-Analyse aus dem Jahr 2012 fasst die Ergebnisse von neun prospektiven Kohortenstudien zusammen, die untersuchen, ob Depression ein Risikofaktor für Hypertonie darstellt. Als primärer Endpunkt wird hierbei die dichotome Variable „Ist eine Hypertonie eingetreten? – ja oder nein“ betrachtet. Der durchschnittliche Beobachtungszeitraum der insgesamt über 22.000 Versuchspersonen, die zu Baselinemessung nicht unter Hypertonie litten, lag bei 9,6 Jahren. Es wird über alle Studien hinweg ein Relatives Risiko von 1,42 ermittelt, sodass das Erkrankungsrisiko bei depressiven Proband:innen 1,42 Mal größer ist als bei Personen, die nicht von Depression betroffen sind.1angelehnt an Meng, Lin; Chen, Dongmei; Yang, Yang; Zheng, Yang; Hui, Rutai (2012): Depression increases the risk of hypertension incidence: a meta-analysis of prospective cohort studies. In: Journal of Hypertension 30 (5), S. 842–851. DOI: 10.1097/HJH.0b013e32835080b7.
Da in Fall-Kontrollstudien meist das Verhältnis von erkrankten (Fällen) zu nicht erkrankten (Kontrollen) Proband:innen künstlich festgelegt wird, ergibt es keinen Sinn Risiken, Risikodifferenzen und Relative Risiken zu betrachten. Stattdessen werden die sogenannten Odds betrachtet. Erinnert ihr euch noch daran, dass in Fall-Kontrollstudien retrospektiv die Gruppen der Exponierten und der Nichtexponierten hinsichtlich der untersuchten Krankheit verglichen werden? (Wenn nicht, dann lest nochmal den Abschnitt zu Fall-Kontrollstudien.) Die Odds geben genau diese Quote bzw. diesen Anteil von Erkrankten zu Nichterkrankten (z. B. 2:1 in der Gruppe der Exponierten) in der jeweiligen Gruppe an. Sie sagen also etwas über die Wahrscheinlichkeit, in der jeweiligen Gruppe zu erkranken, aus (daher auch der Name Odds, engl.: Chance).
Das Odds Ratio (deutsch: Chancenverhältnis) setzt die Odds der beiden betrachteten Gruppen (Gruppe 1 der Exponierten vs. Gruppe 2 der Nichtexponierten) zueinander ins Verhältnis
\widehat{OR} = \frac{\widehat{O_1}}{\widehat{O_2}}
und nimmt als Verhältnisschätzer Werte zwischen und \infty an. Ein Odds Ratio von \widehat{OR} \approx 1 sagt aus, dass kein Zusammenhang zwischen der untersuchten Exposition mit einem Risikofaktor und der betrachteten Krankheit besteht. Eine \widehat{OR} =2,5 sagt aus, dass die Proband:innen in Gruppe 1 der Exponierten eine 2,5 Mal so große „Chance“ haben, an der untersuchten Krankheit zu erkranken als in Gruppe 2 der Nichtexponierten. Somit bestimmt also die Größe des \widehat{OR} < 1 vs. \widehat{OR} > 1 die Richtung des Zusammenhangs.
Insbesondere für die Untersuchung von seltenen Erkrankungen (Inzidenz der Erkrankung bis zu 1 %) bietet das Odds Ratio in Fall-Kontrollstudien eine gute Approximation für das Relative Risiko in Kohortenstudien.
Beispiel: Fall-Kontrollstudie
In einer Fall-Kontrollstudie zur Untersuchung des Zusammenhangs des obstruktiven Schlafapnoesyndroms und Hypertonie wurden 63 hypertone Fälle mit 63 normotonen Kontrollen hinsichtlich der Häufigkeit der auftretenden Apnoeepisoden (Exposition) verglichen. Während bei 71 % der Fälle (also 45 Proband:innen) in der Vergangenheit Apnoeepisoden aufgetreten sind, war dies bei 38 % der Kontrollen (also 24 Proband:innen) der Fall.
Wir berechnen nun das zugehörige Odds Ratio: Die Odds der Exponierten, also der Anteil der an Hypertonie Erkrankten zu den Nichterkrankten unter den an Schlafapnoe leidenden (also exponierten) Patient:innen, liegt bei \widehat{O_1}=\frac{45}{24} \approx 1,88. Unter den Nichtexponierten (ohne Schlafapnoe) sind 18 Patient:innen in der Fallgruppe (hyperton) und 39 Patient:innen in der Kontrollgruppe (normoton). Die Odds der Nichtexponierten berechnen sich also durch \widehat{O_2}=\frac{18}{39} \approx 0,46.
Das Odds Ratio beträgt somit \widehat{OR} = \frac{\widehat{O_1}}{\widehat{O_2}} \approx \frac{1,88}{0,46} \approx 4,1, sodass die an obstruktiver Schlafapnoe leidenden Patient:innen eine 4,1 Mal so eine große „Chance“ für eine Hypertonie aufweisen als die Nichtexponierten.
Solltet ihr einen Blick in die Originalstudie werfen, werdet ihr feststellen, dass in dieser ein Odds Ratio von 4,8 berichtet wird. Das liegt daran, dass in der durchgeführten Analyse noch andere Kovariablen in einem gemeinsamen Modell berücksichtigt wurden, die wir in unseren Berechnungen des Odds Ratios außer Acht lassen.2angelehnt an Gonçalves, Sandro Cadaval; Martinez, Denis; Gus, Miguel; Abreu-Silva, Erlon Oliveira de; Bertoluci, Carolina; Dutra, Isabela et al. (2007): Obstructive sleep apnea and resistant hypertension: a case-control study. In: Chest 132 (6), S. 1858–1862. DOI: 10.1378/chest.07-1170.
In Querschnittstudien werden die sogenannten Prävalenzen analysiert. Wenn du nochmal nachlesen willst, wie eine Querschnittstudie aufgebaut ist, dann schau im Abschnitt zu den Beobachtungsstudien nach. Die Prävalenz beschreibt die relative Häufigkeit der Erkrankungen in einer untersuchten Gruppe zu einem bestimmten Untersuchungszeitunkt. Sie betrachtet also im Gegensatz zur Inzidenz nicht die Neuerkrankungsrate sondern den aktuellen Krankheitsbestand in der Population. Wir können uns die Prävalenzen in zwei unterschiedlichen Gruppen (z. B. die Gruppe der Exponierten mit einem Risikofaktor und die Gruppe der Nichtexponierten) anschauen und auch hier Differenzschätzer und Verhältnisschätzer ermitteln:
Die Prävalenzdifferenz gibt die Differenz der Prävalenzen der zwei betrachteten Gruppen an
\widehat{PD} = \widehat{P_1} – \widehat{P_2}
und nimmt Werte zwischen (bzw. -100 %) und (bzw. +100 %) an. Eine \widehat{PD} =0,05 = 5 \% (bzw. \widehat{PD} = -5 \%) sagt aus, dass von den Gruppenmitgliedern der ersten Gruppe 5 % mehr (bzw. weniger) erkrankt sind als von Gruppe 2.
Das Prävalenzratio gibt den Quotient der Prävalenzen in den beiden Gruppen an:
\widehat{PR} = \frac{\widehat{P_1}}{\widehat{P_2}}
Wie auch die anderen Verhältnisschätzer nimmt es Werte zwischen 0 und \infty an und sagt aus, wie Mal häufiger (\widehat{PR} > 1) oder seltener (\widehat{PR}<1) Erkrankungen in der Gruppe der Exponierten im Vergleich zur anderen Gruppe auftreten. Auch hier weist eine Prävalenzdifferenz \widehat{PD} \approx 0 bzw. Prävalenzratio \widehat{PR} \approx 1, darauf hin, dass kein Unterschied zwischen den betrachteten Gruppen vorliegt und \widehat{PD} \pm 1 bzw. \widehat{PR} = 0 oder \widehat{PR} =\infty sprächen für einen maximalen Gruppenunterschied in die jeweilige Richtung.
Beispiel: Querschnittstudie
Eine Querschnittstudie aus dem Jahr 2015 untersucht die Prävalenz von Hypertonie in vier afrikanischen Staaten südlich der Sahara hinsichtlich unterschiedlicher Risikofaktoren. Insgesamt wurde eine Prävalenz von 25,9 % beobachtet. Ergebnisse hinsichtlich der Risikofaktoren waren unter anderem ein Prävalenzratio von 2,28, also 2,28 Mal häufigere Erkrankung an Hypertonie bei Stadtbewohner:innen im Vergleich zu Bewohner:innen des ländlichen Ugandas. Außerdem wurde ein Prävalenzratio von 1,7 bei Raucher:innen von ungefiltertem Tabak im Vergleich zu Nichtraucher:innen und ein Prävalenzratio von 2,11 bei übergewichtigen Patient:innen im Vergleich zu Patient:innen mit BMI unter 25 kg/m2 festgestellt.3angelehnt an Guwatudde, David; Nankya-Mutyoba, Joan; Kalyesubula, Robert; Laurence, Carien; Adebamowo, Clement; Ajayi, IkeOluwapo et al. (2015): The burden of hypertension in sub-Saharan Africa: a four-country cross sectional study. In: BMC Public Health 15 (1), S. 1211. DOI: 10.1186/s12889-015-2546-z.
Zusatzwissen
Übrigens: Es ist auch möglich, in Kohortenstudien und RCTs mithilfe erhobener Baselinewerte zu Studienbeginn Prävalenzen zu berechnen. Grundsätzlich wird diese Kenngröße dann aber nur zu weiteren Informationszwecken angeführt und nicht in Bezug auf das eigentliche Studienziel.
Nominales Outcome
Wir kennen nominale Variablen als Variablen mit zwei oder mehr Kategorien als Ausprägungen, wobei die Kategorien nicht in eine sinnvolle Ordnung gebracht werden können. Die passenden Effektschätzer für dichotome Outcomes, also nominale Variablen mit genau zwei Ausprägungen, haben wir bereits im letzten Abschnitt betrachtet. Wie aber gehen wir mit mehr als zwei Kategorien um?
Eine Möglichkeit ist es, die Ausprägungen zu genau zwei Gruppen zusammenzufassen und damit einen paarweisen Vergleich der Kategorien wie im dichotomen Fall zu ermöglichen. Eine andere Möglichkeit ist es, die für unsere Fragestellung bedeutendste Kategorie als Referenzkategorie zu wählen und diese gegen die anderen Kategorien zu vergleichen.
Haben wir uns für eine dieser Methoden entschieden, können wir die passenden Effektschätzer je nach Studientyp wählen, wie im letzten Abschnitt zu den dichotomen Outcomes beschrieben. Wir wollen an dieser Stelle nicht weiter auf nominale Outcomes und andere Umgangsmethoden mit ihnen eingehen, aber haben durch diese Form der Umformulierung eine Methode gefunden, die besonders bei recht simplen Fragestellungen schnell Abhilfe schaffen kann.
Ordinales oder nicht-normalverteiltes metrisches Outcome
Ordinale Variablen weisen zwei oder mehr Kategorien auf, die sich ordnen lassen. Wollen wir den Unterschied zwischen zwei Gruppen quantifizieren, bietet es sich also an, zu vergleichen, welche der zu ordnenden Kategorien genau im Zentrum unserer Beobachtungen pro Gruppe liegt. Genau diese Erkenntnis liefert uns der Median. Wir vergleichen also die Mediane pro Gruppe, sodass sich die Differenz der Mediane zwischen Gruppe 1 und Gruppe 2 als geeigneter Effektschätzer ergibt:
\widehat{MedD} = {Med}_1 – {Med_2}
Auch für nicht-normalverteilte metrische Outcomes kann die Differenz der Mediane der zwei Gruppen ein passender Effektschätzer sein. Der Mittelwert, der wie im nächsten Abschnitt beschrieben wird, bei normalverteilten metrischen Variablen zum Einsatz kommt, liefert in diesem Fall weniger präzise Ergebnisse, da er sehr empfindlich auf Ausreißer und nicht symmetrische Daten reagiert. In diesen Fällen bietet der Median eine realistischere Einschätzung über die Verteilung der Daten.
Wir werden im Rahmen des EpiBioManuals nicht weiter auf den Gebrauch dieses Effektschätzers eingehen. Diese Erläuterung soll euch nur eine grobe Vorstellung davon geben, wie mit ordinalen oder nicht-normalverteilten metrischen Outcomes umgegangen werden kann.
Metrisches normalverteiltes Outcome
Für den weiteren Verlauf des EpiBioManuals relevant ist der Umgang mit metrischen normalverteilten Outcomes. Wollen wir zwei voneinander unabhängige Gruppen hinsichtlich dieser Outcomes miteinander vergleichen, können wir die Mittelwerte der zwei Gruppen zu Rate ziehen. Wir wissen, dass der Mittelwert lediglich eine Schätzung auf Basis der Stichprobendaten darstellt. Er schätzt den tatsächlichen Erwartungswert der Grundgesamtheit.
Nachdem wir die Stichprobendaten der zwei Gruppen (in unserem Beispiel die Experimentalgruppe und Kontrollgruppe) erhoben haben, können wir die Mittelwerte der untersuchten Variable pro Gruppe und ihre Differenz ermitteln:
\widehat{MD}= \bar{x_1} – \bar{x_2}
Diese Mittelwertsdifferenz (\widehat{MD}) ist ein geeigneter Effektschätzer, um den Gruppenunterschied zwischen z. B. einer Interventionsgruppe und einer Kontrollgruppe zu quantifizieren und im nächsten Schritt auf Signifikanz zu testen.
Beispiel "Blutdrucksenker"
In unserer Beispielstudie zur Wirkung des Blutdruck senkenden Medikaments wird eine RCT durchgeführt. Im Abschnitt zum t-Test kommt in diesem Kontext auch die Mittelwertsdifferenz als Effektschätzer zum Einsatz, da der metrische und normalverteilte primäre Endpunkt BD_senk (also die Senkung des systolischen Blutdrucks nach 5 Wochen im Vergleich zum Baselinewert) betrachtet wird.
Aus der Datenerhebung ergeben sich die folgenden Werte: Die mittlere Blutdrucksenkung in der Interventionsgruppe beträgt \bar{x_I} \approx 25,61 \text{ mmHg} und in der Kontrollgruppe \bar{x_K} \approx 21,23 \text{ mmHg}. Damit ist unser Schätzer für die Mittelwertsdifferenz \widehat{MD}=25,61-21,23=4,38 \text{ mmHg}.
Outcome auf der Ereigniszeitskala
Für Outcomes auf der Ereigniszeitskala kommen verschiedene Effektschätzer in Frage, um den Unterschied zwischen zwei voneinander unabhängigen Gruppen zu untersuchen. Ein möglicher Effektschätzer ist die Differenz der medianen Ereigniszeiten, wie im Falle eines ordinalen Outcomes. Auch die Differenz der Ereignisraten zu bestimmten Zeitpunkten vergleichbar mit der Risikodifferenz \widehat{RD} kommt als Effektschätzer in Frage.
Das Äquivalent zum Relativen Risiko \widehat{RR} und ein weiterer möglicher Effektschätzer ist das sogenannte Hazard Ratio \widehat{HR}. Das Hazard Ratio lässt sich als Verhältnisschätzer durch den Quotient zwischen den Hazardraten der zwei Gruppen ermitteln:
\widehat{HR}=\frac{{Hazardrate}_1}{{Hazardrate}_2}.
Eine Hazardrate gibt dabei an, wie groß die Wahrscheinlichkeit für das Eintreten des betrachteten Ereignisses zu einem bestimmten Zeitpunkt ist. Es ist gar nicht so einfach, diese Wahrscheinlichkeit zu ermitteln, da sie durch die Auswertung verschiedener Funktionen zu einem bestimmten Zeitpunkt zustande kommt. An dieser Stelle genügt es allerdings, das grobe Konzept und die Interpretation dieses Effektschätzers zu verstehen. Wie auch bei den anderen betrachteten Verhältnisschätzern, weist ein Hazard Ratio \widehat{HR} \approx 1 darauf hin, dass kein Unterschied zwischen den Ereigniswahrscheinlichkeiten der betrachteten Gruppen an dem bestimmten Zeitpunkt vorliegt.
\widehat{HR}=0 oder \widehat{HR} = \infty sprächen für einen maximalen Gruppenunterschied in die jeweilige Richtung.
Zusammenfassung
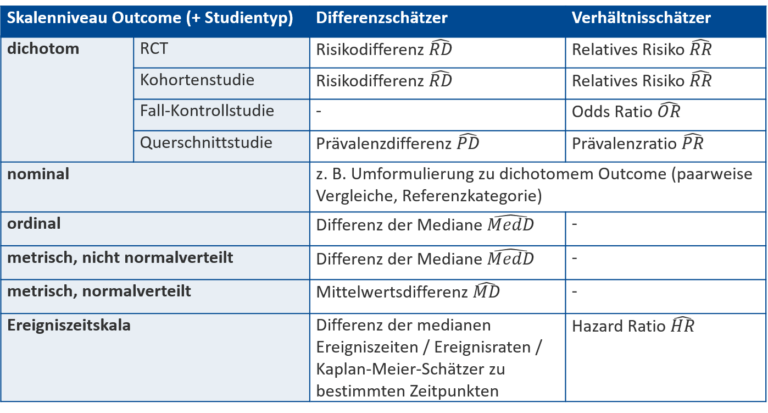
Die folgende Grafik (Abb. 1) fasst nochmal das gesamte Kapitel zu den Effektschätzern auf einen Blick zusammen. Macht euch noch einmal klar, dass es sich bei allen Differenzschätzern und Verhältnisschätzern um Schätzwerte auf Basis der vorliegenden Stichprobendaten handelt.
LITERATURVERZEICHNIS
Die Inhalte dieser Seite sind angelehnt an:
