Statistische Tests

Studienauswertung

Seitenübersicht

Ausgewählte statistische Tests
Zusammenfassung je Testschritt
Weitere Themen im Zusammenhang mit statistischen Tests

Wie bereits erwähnt, ist das Ziel der Inferenzstatistik, mithilfe der Stichprobe auf allgemeingültige Aussagen über die Grundgesamtheit zu schließen. Dazu werden im Vorhinein Forschungshypothesen über die Grundgesamtheit aufgestellt und mithilfe eines geeigneten statistischen Tests auf Basis der Stichprobendaten überprüft.

Im Folgenden werden drei verschiedene Testverfahren im Detail und anhand unseres Beispiels betrachtet: Der Chi-Quadrat-Test (mit einer Einführung in den allgemeinen Ablauf statistischer Tests), der t-Test für unabhängige Stichproben und der Log Rank-Test.

Schaut euch am besten zuerst die Erläuterungen und Beispiele zu den drei Testverfahren an und lest dann weiter.

Chi-Quadrat-Test

Wir schauen uns nun den genauen Ablauf eines statistischen Tests im Detail an. Dazu werden wir anhand unseres Beispiels zum Blutdruck senkenden Medikament einen Chi-Quadrat-Test durchführen.

Beispiel "Blutdrucksenker"

In unserer Beispielstudie zur Untersuchung eines Blutdrucksenkers könnte es z. B. von Interesse sein, zu überprüfen, ob in der Gruppe, die die neue Intervention als Blutdrucksenker bekommen haben, ein größerer Anteil nach 5 Wochen einen Blutdruck im Normbereich aufweist als in der Kontrollgruppe (Standardtherapie). Wir betrachten als primären Endpunkt also die dichotome Variable „Blutdruck bis zum Studienende in den Normbereich (< 140 mmHg) gesunken?“ (BD_norm) mit den zwei Ausprägungen „ja“ oder „nein“. Es ist zu beachten, dass ein Chi-Quadrat-Test nicht für die Analyse von zensierten Daten geeignet ist. Deshalb werden die 5 Versuchspersonen, die vorzeitig aus der Studie ausgeschieden sind, als fehlende Werte deklariert und aus der Analyse ausgeschlossen. Der später thematisierte Log Rank-Test hat hingegen den Vorteil, dass er zensierte Daten angemessen berücksichtigt.

Im ersten Schritt werden die zu testenden Hypothesen aufgestellt. Wie man eine inhaltliche Forschungshypothese formuliert, haben wir im Abschnitt Forschungshypothesen schon gelernt. Es werden genau zwei Hypothesen aufgestellt. Diese beiden Hypothesen heißen Nullhypothese und Alternativhypothese und komplementieren sich gegenseitig. Das heißt, die Nullhypothese ist das Gegenteil der Alternativhypothese.
In der Nullhypothese ( $H0$ ) wird in dem von uns betrachteten Fall von Unterschiedshypothesen angenommen, dass sich zwei Gruppen nicht unterscheiden. In der Alternativhypothese ( $H1$ ) steht das Gegenteil, also, dass sich die Gruppen unterscheiden. Damit steht in der Alternativhypothese das, was wir im besten Fall durch unseren Test zeigen wollen, indem wir die Nullhypothese ablehnen und damit auf die Alternativhypothese schließen. Wie genau es zur Ablehnung der Nullhypothese kommt, werdet ihr im weiteren Verlauf dieses Abschnitts lernen.

ACHTUNG: Können wir die Nullhypothese nicht verwerfen, dann spricht das nicht automatisch für die Annahme der Nullhypothese und das Ablehnen der Alternativhypothese. Wir können dann lediglich schließen, dass wir die Nullhypothese nicht ablehnen konnten und haben damit keine Erkenntnis über einen signifikanten Unterschied gewon-nen.
Wie sehen nun die konkreten Unterschiedshypothesen aus? H0 beschreibt in diesem Fall: „Es gibt keinen Unterschied zwischen den betrachteten Gruppen“. H1 bezeichnet das Gegenteil: „Es gibt einen Unterschied zwischen den Gruppen“.

Beispiel "Blutdrucksenker"

Geeignete inhaltliche Nullhypothese und Alternativhypothese für unser Beispiel sind:

$H0$ : „Der Anteil an Patient:innen, bei denen der Blutdruck nach 5 Wochen in den Normbereich gesunken ist, unterscheidet sich nicht zwischen Interventions- und Kontrollgruppe (neue Intervention vs. Standardtherapie).“

versus

$H1$ : „Der Anteil an Patient:innen, bei denen der Blutdruck nach 5 Wochen in den Normbereich gesunken ist, unterscheidet sich zwischen Interventions- und Kontrollgruppe.“

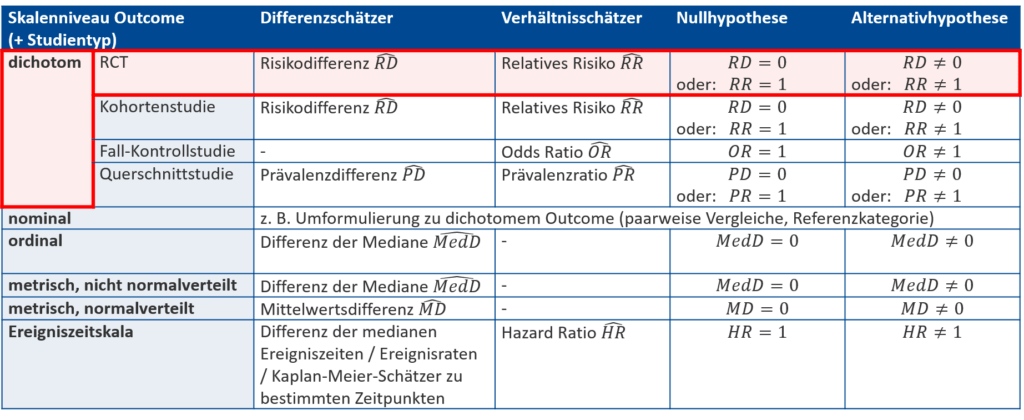
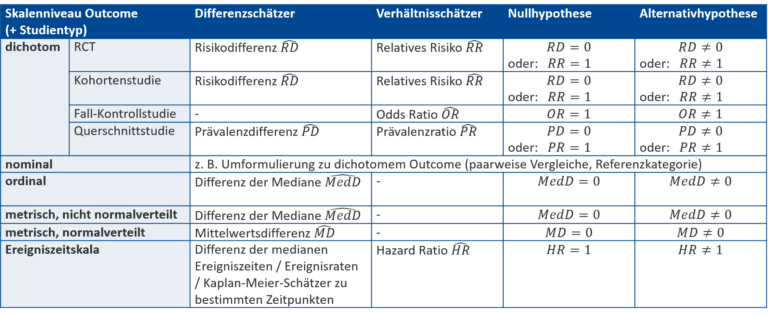
Statistische Hypothesen sind das mathematisch formulierte Äquivalent zu den inhaltlichen Forschungshypothesen. Wir schauen uns nun die Formulierung von statistischen Hypothesen mithilfe der zum Skalenniveau und Studientyp passenden Effektschätzer an. Die untenstehende Tabelle kennt ihr bereits aus dem Abschnitt zu den Effektschätzern. Sie wurde jetzt um zwei Spalten erweitert: die passende statistische Null- und Alternativhypothese, die auf einen Unterschied ohne spezifische Richtung testen. Die Nullhypothese geht von keinem Unterschied zwischen den betrachteten Gruppen aus. Somit findet sich entweder keine Differenz ( $\text{Differenz}=0$ ) oder das betrachtete Verhältnis ist 1:1 ( $\text{Verhältnis}=1$ ), was dann eintritt, wenn Zähler und Nenner gleiche Werte annehmen. Die Alternativhypothese geht von dem vermuteten Unterschied aus und wird genau als Gegenteil der Nullhypothese formuliert ( $\text{Differenz} \neq 0$ , $\text{Verhältnis} \neq 1$ ).

Zur Erinnerung:
Die Effektschätzer selbst sind wie der Name schon sagt, Schätzungen, die auf Basis der Daten der Stichprobe geschätzt werden. Um sie als solche zu erkennen, werden sie mit einem Dach (z. B. $\widehat{RD}$ ) beschriftet. Auch der Mittelwert $\overline{x}$ stellt einen Schätzer dar.

Die statistischen Hypothesen stellen hingegen Vermutungen über die anvisierte Grundgesamtheit dar. Sie werden also mithilfe der wahren Werte des vermuteten Effekts formuliert, die ohne Dach (z. B. $RD$ ) geschrieben werden. Der Erwartungswert der Grundgesamtheit $\mu$ ist das Pendant zum Mittelwert $\overline{x}$ .

Beispiel "Blutdrucksenker"

Wir nutzen die Übersicht (Abb. 1), um die passenden statistischen Hypothesen für unsere Beispielstudie aufzustellen: Es handelt sich bei BD_norm um ein dichotomes Outcome mit den zwei Ausprägungen „ja“ und „nein“. Des Weiteren führen wir eine randomisierte kontrollierte Studie (RCT) durch. Somit werden Risiken betrachtet. Zwei mögliche Hypothesenpaare für zu testende statistische Hypothesen sind:

$H0: RD= 0$ versus $H1: RD \neq 0$
$H0: RR= 1$ versus $H1: RR \neq 1$

Der zweite Schritt ist das Festlegen eines geeigneten Signifikanzniveaus

\alpha

. Wenn wir einen statistischen Test durchführen, kann dieser entweder richtige oder falsche Ergebnisse liefern. Der Test liefert das richtige Ergebnis, wenn

H0

in Wahrheit richtig (bzw. falsch) ist und auch der Test von einer richtigen (bzw. falschen) Nullhypothese ausgeht. Auf der anderen Seite gibt es zwei mögliche Fehler bei der Durchführung eines statistischen Tests: Der Fehler 1. Art (oder auch

\alpha

-Fehler) tritt ein, wenn

H0

in Wahrheit richtig ist, wir sie aber fälschlicherweise ablehnen. Der Fehler 2. Art (oder auch

\beta

-Fehler) beschreibt den Fall, dass die Nullhypothese in Wahrheit falsch ist und wir sie ablehnen könnten, stattdessen aber beibehalten. Wir übersehen also die Möglichkeit auf Ablehnung der Nullhypothese. Die beschriebenen Fälle sind in Tab. 1 zusammengefasst.

Tab. 1: Testentscheidung vs. Realität (mögliche Fälle und ihre jeweilige Wahrscheinlichkeit)
		Realität
		$H0$ wahr	$H1$ wahr
Testentscheidung für …	$H0$	Richtig (Grad an gewünschter Sicherheit): $1-\alpha$	Fehler 2. Art: $\beta$
Testentscheidung für …	$H1$	Fehler 1. Art: $\alpha$	Richtig (Power): $1-\beta$

Die Wahrscheinlichkeit

1-\beta

, also die Wahrscheinlichkeit, eine in Wahrheit korrekte Alternativhypothese auch durch Ablehnung von

H0

als solche zu identifizieren, wird häufig als Power oder Güte des Tests bezeichnet. Die Wahrscheinlichkeit

1-\alpha

wird als Gegenwahrscheinlichkeit zur Irrtumswahrscheinlichkeit

\alpha

oft Grad an gewünschter Sicherheit genannt.

Beispiel "Blutdrucksenker"

Bezogen auf unser Beispiel bedeutet ein Fehler 1. Art, dass wir davon ausgehen, dass der Anteil der Patient:innen, deren Blutdruck in den Normbereich gesenkt werden konnte, sich zwischen beiden Gruppen unterscheidet (die neue Therapie funktioniert angeblich besser oder schlechter als die Standardtherapie), obwohl in Wirklichkeit kein Unterschied zwischen den beiden Therapien besteht.

Der Fehler 2. Art würde bedeuten, dass wir den Fakt, dass in der Interventionsgruppe mehr oder weniger Patient:innen in den Normbereich gesenkt werden konnten als durch die Standardtherapie übersehen und fälschlicherweise von vergleichbaren Ergebnissen ausgehen. Dies könnte z. B. zur Folge haben, dass wir eine eigentlich besser funktionierende neue Therapie nicht weiter anwenden.

Der Fehler 1. Art kann in der Analyse kontrolliert werden, d. h. man legt ihn durch das Signifikanzniveau $\alpha$ fest und wählt das entsprechende Quantil für das Konfidenzintervall bzw. den entsprechenden kritischen Wert für den statistischen Test, auf den im weiteren Verlauf des Abschnitts eingegangen wird. Den Fehler 2. Art kann man dagegen nur in der Planung durch die Wahl der Stichprobengröße beeinflussen. Wenn man eine Fallzahlplanung, die später genauer erläutert wird, durchführt, kann man die gewünschte Power $1-\beta$ festlegen und weiß dann, wie viele Studienteilnehmer benötigt werden, um diese Power zu erzielen.
Ein typischer Wert für das Signifikanzniveau ist $\alpha = 5 \%$ . Ist es in deinem Test besonders wichtig, dass keine falschen Schlüsse gezogen werden, kann $\alpha$ weiter reduziert werden. Dann würde allerdings wieder eine größere Fallzahl benötigt werden, um die gewünschte Power zu erzielen.

Beispiel "Blutdrucksenker"

Wir legen auch in unserer Beispielstudie ein Signifikanzniveau von $\alpha = 5 \%$ fest.

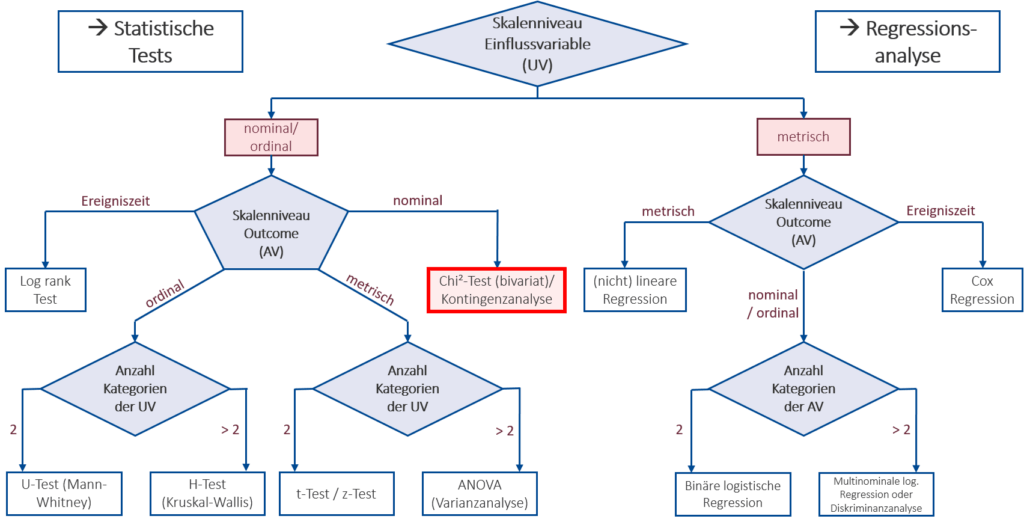
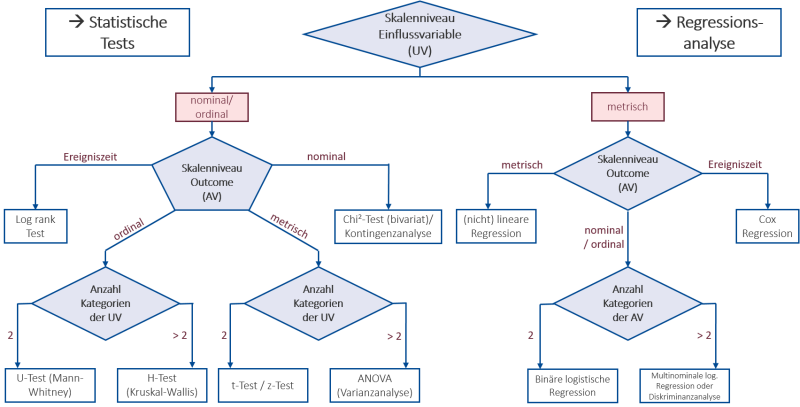
Der dritte Schritt ist die Auswahl eines geeigneten Testverfahrens und der damit einhergehenden Teststatistik. Welches Verfahren, also welcher statistische Test, geeignet ist hängt von dem Skalenniveau (und anderen Eigenschaften) der vorliegenden Daten und den Hypothesen ab. Es ist sinnvoll, zur Orientierung auf eine geeignete Übersicht wie in Abb. 2 zurückzugreifen. Das damit ausgewählte Testverfahren bringt die jeweils zu bestimmende Teststatistik mit sich, auf die in den nächsten Schritten genauer eingegangen wird.

Beispiel "Blutdrucksenker"

In unserem Beispiel wird mit der „Gruppenzuteilung“ eine dichotome, also nominale Einflussvariable betrachtet, somit bewegen wir uns bei der ersten Abzweigung nach links. Es wird der Effekt der Gruppenzuteilung auf die ebenfalls nominale, dichotome Variable „Blutdruck in den Normbereich ( $< 140\text{ mmHg}$ ) gesunken?“ (BD_norm) untersucht. Somit wählen wir die Abzweigung nach rechts. Wie in der Abbildung zu sehen, ist damit der bivariate Chi-Quadrat-Test ein geeignetes Testverfahren.

Bevor im vierten Schritt die Teststatistik und der dazugehörige $p$ -Wert berechnet werden können, müssen zunächst die Daten erhoben werden. Es ist wichtig, dass die ersten drei Schritte bereits vor der Datensammlung abgearbeitet werden, damit keine Verfälschung der Testergebnisse durch eine datenbasierte Methodenwahl auftritt. So wäre es keine gute wissenschaftliche Praxis erst die Daten zu erheben und dann nach geeigneten Fragestellungen zu suchen, die sich aufgrund der vorliegenden Daten zum Vorteil der Forschenden beantworten lassen.

Beispiel "Blutdrucksenker"

Die erhobenen Daten unserer Beispielstudie, aufgeführt in einer Vierfeldertafel in Tab. 2, kennt ihr schon aus dem Abschnitt zu den Effektschätzern. Wie gesagt, werden von den insgesamt 100 Patient:innen nur 95 weiter betrachtet, da die anderen frühzeitig aus der Studie ausgeschieden sind und damit keine Messwerte nach 5 Wochen vorliegen.

Tab. 2: Vierfeldertafel der Beispieldaten
Empirische Daten	Blutdruck auf < 140 mmHg gesunken	Blutdruck nicht auf < 140 mmHG gesunken	Summe
Neue Intervention (Intervention)	$a=40$	$b=6$	46
Standardtherapie (Kontrolle)	$c=32$	$d=17$	49
Summe	72	23	$n=95$

Die bereits ermittelten Effektschätzer betragen

\widehat{RD} \approx 0,22

und

\widehat{RR}\approx 1,34

. Diese Schätzungen und sogar das bloße Betrachten der erhobenen Daten lässt vermuten, dass die neue Intervention eine bessere Blutdruck senkende Wirkung mitbringt als die Standardtherapie (

\widehat{RD} >0

und

\widehat{RR}>1

). Ob es sich dabei allerdings um einen systematischen Unterschied handelt, sich die Gruppen also signifikant voneinander unterscheiden, lässt sich nur mithilfe eines statistischen Tests beantworten.

Der vierte Schritt des eigentlichen Tests ist die Berechnung der Teststatistik. Die Teststatistik kann als eine Maßzahl gesehen werden, die die Studienergebnisse in einem Wert zusammenfasst. Sie wird anhand einer zum jeweiligen Testverfahren gehörenden Berechnungsformel aus den vorliegenden Daten ermittelt.
Für den Chi-Quadrat-Test wird die Teststatistik anhand der beobachteten (Tabelle 1) und der unter Unabhängigkeit erwarteten Werte (Tabelle 2, siehe unten) mit der folgenden Formel berechnet:

$X^2=a_{diff}+b_{diff}+c_{diff}+d_{diff}$

mit $a_{diff}=\frac{(a-a_{erw})^2}{a_{erw}}$ und $b_{diff}$ , $c_{diff}$ , $d_{diff}$ analog.

Die Daten unter Unabhängigkeit sind die Ergebnisse, die wir erwartet hätten, wenn es zwischen den beiden betrachteten Gruppen keinen Zusammenhang geben würde, was in unserem Beispiel nochmal genauer erläutert wird.

Beispiel "Blutdrucksenker"

Um die Teststatistik zu berechnen, ermitteln wir zuerst die Tabelle der Daten unter Unabhängigkeit: Hätten wir die gleichen Ergebnisse (also 72 Patient:innen mit in den Normbereich gesunkenem Blutdruck und 23 Patient:innen mit weiterhin zu hohem Blutdruck) ohne einen Wirkungsunterschied zwischen den zwei Gruppen (neue Intervention vs. Standardtherapie) beobachtet, hätten wir die folgende Tabelle beobachtet:

Tab. 3: Vierfeldertafel Daten unter Unabhängigkeit
Daten unter Unabhängigkeit	Blutdruck auf < 140 mmHg gesunken	Blutdruck nicht auf < 140 mmHG gesunken	Summe
Neue Intervention (Intervention)	$a_{erw}=34,86$	$b_{erw}=11,14$	46
Standardtherapie (Kontrolle)	$c_{erw}=37,14$	$d_{erw}=11,86$	49
Summe	72	23	$n=95$

Man spricht von den Daten unter Unabhängigkeit, da in diesem Fall die Senkung des Blutdrucks unabhängig von der Gruppenzuteilung ist. Wir sehen im ersten Schritt, dass die Werte am Rand der Tabelle gleichgeblieben sind und nur die Werte im Inneren der Tabelle variieren, die wir nun im zweiten Schritt ermitteln werden. Wenn wir wissen, dass von den insgesamt 95 Patient:innen 72 bei Studienende in den Normbereich gesenkt werden konnten, sind das $75,79 \%$ . Genau diesen Anteil würden wir in beiden Behandlungsgruppen erwarten, wenn die neue Intervention die gleiche Blutdruck senkende Wirkung hätte wie die Standardtherapie. Die Tabelle spiegelt also das wider, was wir erwartet hätten, wenn die Nullhypothese stimmen würde. In der Interventionsgruppe würden wir also bei $46 \cdot 75,79 \% \approx 34,86$ Patient:innen eine Senkung in den Normbereich erwarten, in der Kontrollgruppe bei $49 \cdot 75,79 \% \approx 37,14$ Patient:innen.

Nun wollen wir die Teststatistik mithilfe der oben genannten Formel berechnen:

$X^2=a_{diff}+b_{diff}+c_{diff}+d_{diff}$

$=\frac{(40-34,86)^2}{34,86}+\frac{(6-11,14)^2}{11,14}+\frac{(32-37,14)^2}{37,14}+\frac{(16-11,86)^2}{11,86}$

$\approx 0,76 + 2,37 + 0,71 + 2,23 \approx 6,07.$

Im nächsten Schritt wird eine Testentscheidung getroffen. Dafür gibt es zwei Möglichkeiten: Entweder man vergleicht die berechnete Teststatistik mit dem sogenannten kritischen Wert oder man bestimmt den sogenannten $p$ -Wert zur berechneten Teststatistik.

Für den Vergleich von Teststatistik und kritischem Wert wird geschaut, ob sich der empirische Wert der Teststatistik innerhalb oder außerhalb des Ablehnungsbereichs befindet. Befindet er sich im Ablehnungsbereich, kann, daher der Name, die Nullhypothese abgelehnt werden. Der Ablehnungsbereich umfasst all die Beobachtungen an den Rändern der Verteilung, die zusammengerechnet maximal eine Wahrscheinlichkeit von $\alpha$ aufweisen. Da die Chi-Quadrat-Verteilung nur nicht-negative Werte annehmen kann (da die Bestandteile der Teststatistik aus quadrierten Differenzen basieren), befindet sich der Ablehnungsbereich in unserem Fall nur auf der rechten Seite der Verteilung. Bei anderen statistischen Tests hingegen (z. B. einem zweiseitigen t-Test, wie wir später sehen werden) kann er auch auf die linke und rechte Seite der Verteilung verteilt sein, aber die Fläche unter der Verteilung weist trotzdem nur zusammengerechnet eine Wahrscheinlichkeit von $\alpha$ auf.

Beispiel "Blutdrucksenker"

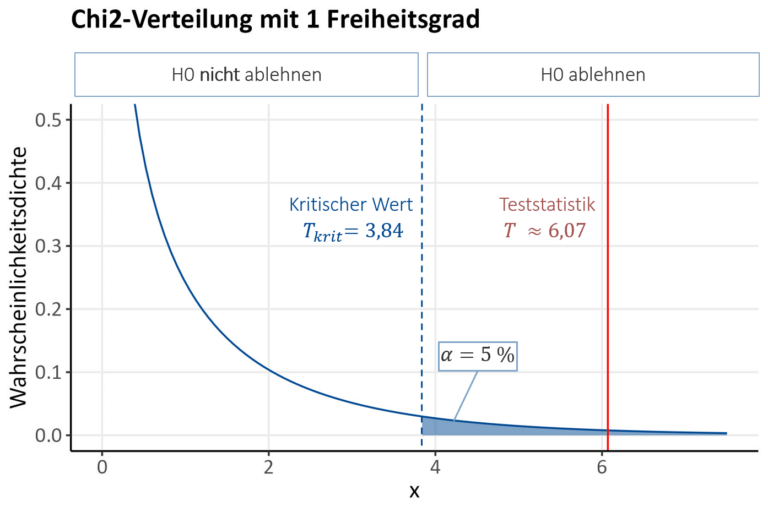
Der genaue Wert, bei dem der Ablehnungsbereich beginnt, wird als kritischer Wert $T_{krit}$ bezeichnet und durch das $(1-\alpha)$ –Quantil der Chi-Quadrat-Verteilung mit $df = (k-1)\cdot(l-1)$ Freiheitsgraden ermittelt. Dabei sind $l$ und $k$ die Anzahl an Kategorien der abhängigen und der unabhängigen Variablen. Die Anzahl der Freiheitsgrade gibt an, bei wie vielen Parametern der/die Anwender:in die „Freiheit“ hat, diese nach eigenem Ermessen zu verändern bzw. festzulegen.

Beispiel "Blutdrucksenker"

In unserem Beispiel weisen abhängige und unabhängige Variablen jeweils 2 Kategorien auf, damit sind also $l = k = 2$ und es ergibt sich $df=(2-1) \cdot (2-1) = 1$ Freiheitsgrad.

Die Verteilungstabelle (PDF) liefert uns für das 95 %-Quantil der Chi-Quadrat-Verteilung mit einem Freiheitsgrad den kritischen Wert $T_{krit}\approx 3,84$ . Wenn die Teststatistik größer als der kritische Wert ist, würde man also die Nullhypothese ablehnen und hätte einen signifikanten Unterschied gezeigt.

Alternativ kann die Testentscheidung mit Hilfe des $p$ -Werts getroffen werden. Der $p$ -Wert gibt die Wahrscheinlichkeit dafür an, dass, wenn die Nullhypothese wahr ist, die beobachtete oder eine noch extremere Teststatistik auftritt. Ihr müsst diesen Wert nicht selbst berechnen, sondern es genügt seine Interpretation zu kennen und mit seiner Hilfe Testentscheidungen zu treffen (darauf wird im nächsten Schritt eingegangen). ACHTUNG: Der $p$ -Wert macht keine Aussagen über die Relevanz des Ergebnisses für die Praxis (siehe Abschnitt Signifikanz vs. Relevanz), über kausale Zusammenhänge oder über die Stärke des untersuchten Effekts.

Beispiel "Blutdrucksenker"

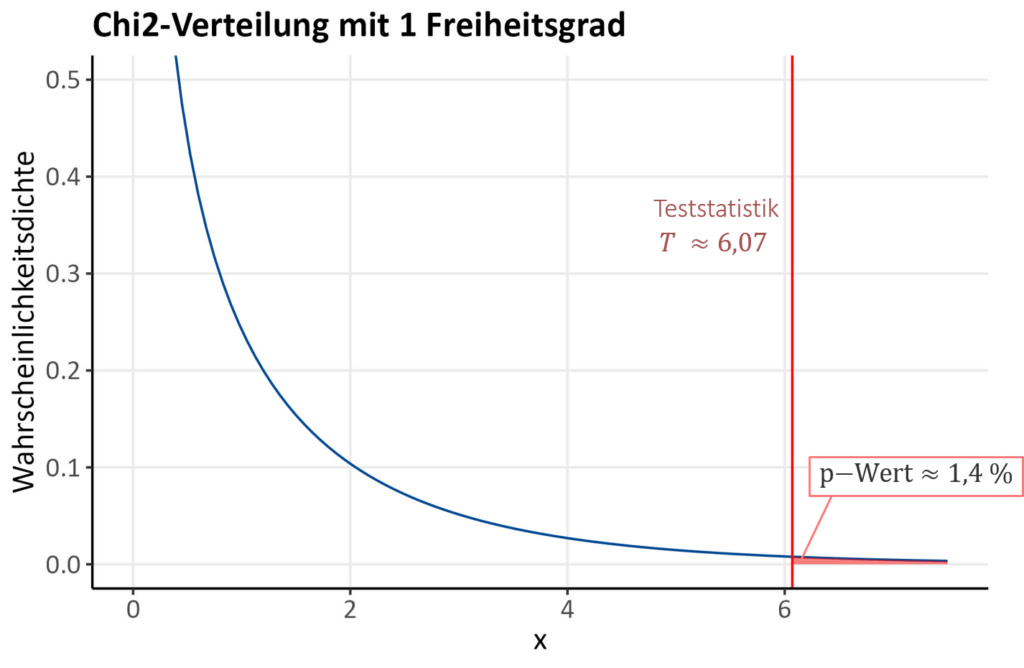
In unserem Beispiel ergibt sich ein $p$ -Wert für die Teststatistik von $X^2 \approx 6,07$ von $p\text{-Wert}=0,014 = 1,4\%$ , was der Fläche unter der Kurve rechts von der Teststatistik entspricht (in Abb. 4 in hellrot gekennzeichnet und beschriftet). Das bedeutet, die Wahrscheinlichkeit mit den vorliegenden Daten die gleiche (oder eine noch extremere) Teststatistik zu erhalten, wenn $H0$ stimmen würde, liegt bei ca. $1,4 \%$ . Da es sich um eine kleine Wahrscheinlichkeit handelt, spricht dies eher dafür, dass die $H0$ nicht stimmt und abgelehnt werden kann. Sobald der $p$ -Wert kleiner als die vorher festgelegte Wahrscheinlichkeit für den Fehler 1. Art, also das Signifikanzniveau $\alpha$ ist, kann die Nullhypothese abgelehnt und auf einen signifikanten Unterschied geschlossen werden.

Wir haben also zwei Möglichkeiten kennengelernt, um zu entscheiden, ob wir die Nullhypothese ablehnen können oder nicht:

Die erste ist es, die Teststatistik mit dem kritischen Wert zu vergleichen und somit zu schauen, ob sie im Ablehnungsbereich liegt. Wir lehnen also ab, wenn die ermittelte Teststatistik größer als der kritische Wert ist.
Eine zweite Möglichkeit ist es, den $p$ -Wert mit dem vorher festgelegten Signifikanzniveau zu vergleichen. Wir lehnen ab, wenn der berechnete $p$ -Wert kleiner als das Signifikanzniveau $\alpha$ ist.
Es gibt noch eine dritte Möglichkeit eine Testentscheidung zu treffen. Diese ist eine Entscheidung mithilfe eines geeigneten Konfidenzintervalls. Betrachten wir in unserer statistischen Hypothese eine Differenz, erfolgt die Ablehnung, wenn unser aus den Daten ermitteltes Konfidenzintervall für den Differenzschätzer die 0 nicht enthält. Wird ein Verhältnis untersucht, erfolgt die Ablehnung, wenn das Konfidenzintervall für den Verhältnisschätzer die 1 nicht beinhaltet.

Mit allen drei Möglichkeiten gelangt man zur selben Entscheidung (außer man hat sich irgendwo verrechnet).

Beispiel "Blutdrucksenker"

Wir gehen nun die 3 Möglichkeiten für unser Beispiel durch:

In unserem Fall ist $T\approx 6,07 > 3,84=T_{krit}$ . Die Teststatistik ist also größer als der kritische Wert. Wir befinden uns damit deutlich im Ablehnungsbereich und können die Nullhypothese ablehnen.
Hier ist der $p\text{-Wert}\approx 1,4 \% < 5\%=\alpha$ und wir kommen auch hier zu dem Entschluss, die Nullhypothesen abzulehnen.
In unserem Beispiel haben wir im Kapitel Konfidenzintervalle die folgenden Konfidenzintervalle ermittelt: $95\%\text{-}KI_{RD}=[0,06; 0,38]$ und $95\%\text{-}KI_{RR}=[1,06; 1,70]$ . Analog zu der Entscheidung des statistischen Tests enthält das Konfidenzintervall der Risikodifferenz nicht die 0 und das Konfidenzintervall des Relativen Risikos nicht die 1. Damit können wir auch mithilfe der Konfidenzintervalle die Nullhypothese ablehnen.

Zusatzwissen

Vorteile der Angabe eines Konfidenzintervalls für die Hypothesenprüfung¹

Ihr habt nun verschiedene Wege kennengelernt, wie ihr herausfinden könnt, ob der untersuchte Effekt signifikant ist oder nicht. Die zwei Möglichkeiten, zu gucken, ob die Teststatistik im Ablehnungsbereich liegt oder der $p$ -Wert kleiner als das festgelegte Signifikanzniveau ist, hängen direkt mit dem durchgeführten statistischen Test zusammen. Eine weitere Möglichkeit der Hypothesenüberprüfung kann über Konfidenzintervalle erfolgen. Die Methode bringt zwei große Vorteile mit sich:

Konfidenzintervalle informieren im Gegensatz zum $p$ -Wert direkt über die Richtung des untersuchten Effekts: Enthält das aufgestellte Konfidenzintervall die 0 (Differenzschätzer) bzw. die 1 (Verhältnisschätzer) nicht, handelt es sich um einen signifikanten Effekt und es kann festgestellt werden, ob das gesamte Konfidenzintervall unterhalb oder oberhalb der 0 bzw. der 1 liegt.
Die Grenzen des Konfidenzintervalls sind, erneut im Gegensatz zum $p$ -Wert, in der gleichen Einheit angegeben wie die Effektschätzer selbst und damit leichter interpretierbar. In unserem Beispiel zur Differenz der mittleren Senkung des Blutdrucks zwischen den Behandlungsgruppen werden die obere und untere Grenze des Konfidenzintervalls dementsprechend in mmHg angegeben.

Im letzten Schritt müssen die Ergebnisse noch inhaltlich, also in Bezug auf die konkrete Anwendung, interpretiert werden.

Beispiel "Blutdrucksenker"

Wir schließen bei Ablehnung der Nullhypothese folglich auf die Alternativhypothese und stellen somit fest, dass sich der Anteil an Patient:innen, deren systolischer Blutdruck nach 5 Wochen in den Normbereich ( $<140 \text{ mmHg}$ ) gesunken ist, zwischen der Interventions- und Kontrollgruppe signifikant voneinander unterscheidet.

t-Test für unabhängige Stichproben

Zusatzwissen

Achtung: t-Test vs. z-Test

In einigen statistischen Einführungsveranstaltungen wird der Fokus statt auf den t-Tests auf den z-Test gelegt, da dieser ein wenig einfacher zu verstehen ist. Im Grunde sind sich die beiden Tests in der Durchführung sehr ähnlich und unterscheiden sich nur in wenigen Punkten: Für die Durchführung des z-Tests muss davon ausgegangen werden, dass die tatsächliche Varianz der Grundgesamtheit bekannt ist. Da dies in der Praxis so gut wie nie der Fall ist, wird in Studien eher der t-Test genutzt, der die geschätzten Varianzen auf Basis der Stichprobendaten verwendet. Aus diesem Grund gehen wir hier auf den t-Test und nicht wie in der Vorlesung erneut auf den z-Test ein. Während der z-Test auf der Standardnormalverteilung, die ihr aus dem Abschnitt Normalverteilung kennt, basiert, nutzt der t-Test die sogenannte t-Verteilung. Wie bereits in der Zusatzbox zur t-Verteilung erläutert, unterscheiden sich die beiden Verteilungen für bestimmte Parameter (Freiheitsgrade) und große Stichproben fast gar nicht voneinander.
Ihr werdet im Laufe des Kapitels an den folgenden Stellen kleine Unterschiede zwischen t-Test und z-Test feststellen: Während der kritische Wert beim z-Test nur vom Signifikanzniveau $\alpha$ abhängt, spielen beim t-Test, wie auch beim Chi-Quadrat-Test, die Freiheitsgrade df eine Rolle. Diese müssen beim t-Test mithilfe der Stichprobengröße $n$ ermittelt werden. Somit ergibt sich auch ein anderer $p$ -Wert, da dieser von der zugrundeliegenden Verteilung abhängt.

Im Abschnitt zum Chi-Quadrat-Test haben wir die grundlegenden Schritte eines statistischen Tests kennengelernt und anhand eines Beispiels erläutert. Wie in der Übersicht zu verschiedenen Testverfahren sichtbar wird, kommen je nach Skalenniveau und Anzahl der zu untersuchenden Variablen auch noch viele andere Testverfahren in Frage. Ein weiteres Testverfahren, das wir uns nun genauer anschauen wollen, ist der t-Test für unabhängige Stichproben. Er wird verwendet, um festzustellen, ob sich die Mittelwerte zwischen zwei Gruppen, deren Messwerte unabhängig voneinander sind, signifikant voneinander unterscheiden. Wozu das interessant sein kann, wird in unserer Beispielstudie deutlich:

Beispiel "Blutdrucksenker"

Wir betrachten nun unser vorheriges Beispiel zur Wirkung eines Blutdrucksenkers. Es stellt sich wieder die Frage, ob die neue Intervention eine stärkere (oder schwächere) Blutdruck senkende Wirkung aufweist als die Standardtherapie. Für den Chi-Quadrat Test haben wir uns als dichotomen primären Endpunkt lediglich angeschaut, ob eine Senkung des systolischen Blutdrucks in den Normbereich aufgetreten ist oder nicht. In der Praxis könnte es allerdings relevanter sein, sich die konkreten Messwerte des Blutdrucks anzugucken. Dazu kommt die metrische Variable BD_senk als metrischer primärer Endpunkt ins Spiel: Sie bezeichnet die Differenz aus dem Blutdruck nach 5 Wochen und dem Baselinewert. Beide Gruppen, Interventions- und Kontrollgruppe, haben einen Mittelwert dieser Variablen, der die „mittlere Blutdrucksenkung nach 5 Wochen“ pro Gruppe angibt. Mithilfe des folgenden t-Tests wollen wir untersuchen, ob sich dieser Mittelwert zwischen den Gruppen signifikant voneinander unterscheidet. Wenn ja, spricht das dafür, dass die neue Therapie besser oder schlechter wirkt als die Standardtherapie.

Zunächst werden wieder die inhaltlichen Hypothesenpaare aufgestellt: In der Nullhypothese steht wieder die Ausgangsannahme, dass kein Unterschied zwischen den Gruppen besteht, und in der Alternativhypothese, der sich aus der Forschungshypothese ergebende vermutete Unterschied zwischen den Gruppen.

Beispiel "Blutdrucksenker"

$H0$ : Der Mittelwert der Differenz zwischen dem Blutdruck nach 5 Wochen und dem Baselinewert unterscheidet sich nicht zwischen der Interventions- (I, neues Medikament) und der Kontrollgruppe (K, Standardtherapie).
$H1$ : Der Mittelwert der Differenz zwischen dem Blutdruck nach 5 Wochen und dem Baselinewert unterscheidet sich zwischen der Interventions- (I, neues Medikament) und der Kontrollgruppe (K, Standardtherapie).

Als nächstes wollen wir mithilfe der Übersichtstabelle (Abb. 6) zu den Effektschätzern auch statistische Hypothesen formulieren:

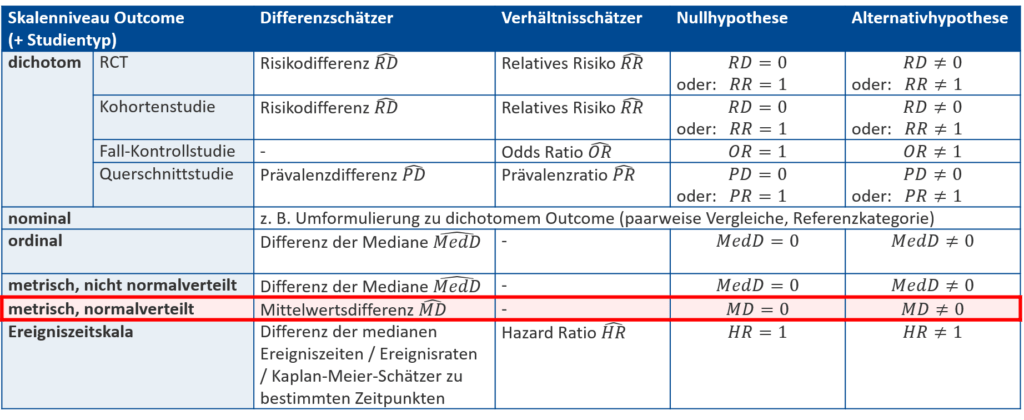
Es handelt in diesem Fall um ein metrisches und pro Behandlungsgruppe normalverteiltes Outcome (siehe Abschnitt zur Normalverteilung). Somit bietet die Mittelwertsdifferenz einen geeigneten Effektschätzer und es können die folgenden statistischen Hypothesen untersucht werden:

$H0\text{: }MD=\mu_I – \mu_K = 0$ versus $H1\text{: }MD=\mu_I – \mu_K \neq 0$

Beispiel "Blutdrucksenker"

Im zweiten Schritt wird auch hier ein Signifikanzniveau von $\alpha=5 \%$ festgelegt.

Als nächstes wird im dritten Schritt ein geeignetes Testverfahren ausgewählt. Weil wir uns Mittelwerte anschauen wollen, bedeutet das im Umkehrschluss, dass der primäre Endpunkt (engl.: Outcome) metrisch skaliert sein muss (im Gegensatz zum Chi-Quadrat-Test, bei dem wir uns eine nominal skalierte Variable angeschaut haben), um überhaupt in der Lage zu sein, Mittelwerte berechnen zu können. Die Einflussvariable hingegen ist, wie beim Chi-Quadrat-Test, nominal skaliert mit 2 Kategorien als Ausprägung, da sie die Zuordnung zu den Gruppen wiedergibt, zwischen denen verglichen werden soll. Somit kommt also der t-Test für unabhängige Stichproben in Frage.

Die zu berechnende Teststatistik für den t-test für unabhängige Stichproben sieht wie folgt aus:

$T=\frac{\overline{x}_1-\overline{x}_2}{SE_{MD}}=\frac{\widehat{MD}}{SE_{MD}}.$

Zusatzwissen

Prüfung der Voraussetzungen für den t-Test für unabhängige Stichproben

Es werden nun nochmal alle Voraussetzungen für die Durchführung eines t-Tests für unabhängige Stichproben geprüft: Die Messungen in den zwei Gruppen sind unabhängig voneinander, denn die Blutdruckwerte der einen Gruppe werden nicht durch die Werte der anderen beeinflusst. Das Ouctome ist metrisch skaliert (Differenz der Blutdruckmesswerte) und pro Gruppe annähernd normalverteilt (siehe Abschnitt zur Normalverteilung). Die letzte zu überprüfende Voraussetzung ist die Varianzgleichheit zwischen den zwei Gruppen (deskriptiver Vergleich).

Im nächsten Schritt werden die Daten erhoben.

Mit der in Schritt 3 genannten Formel wird im vierten Schritt die Teststatistik anhand der vorliegenden Daten berechnet und anschließend der $p$ -Wert ermittelt. In der Praxis geschehen diese Berechnungen meistens nicht von Hand, sondern mit geeigneter statistischer Software.

Beispiel "Blutdrucksenker"

In unserem Beispiel ergeben sich die folgenden Werte (siehe dazu auch Abschnitt Effektschätzer): Die mittlere Blutdrucksenkung in der Interventionsgruppe (Gruppe 1) beträgt $\overline{x}_I \approx 25,61$ und in der Kontrollgruppe (Gruppe 2) $\overline{x}_K \approx 21,23$ . Damit ist unser Schätzer für die Mittelwertsdifferenz $\widehat{MD}=4,38$ . Der Standardfehler der Mittelwertsdifferenz ist gegeben durch $SD_{MD} \approx 1,43$ (auf die Herleitung wird an dieser Stelle verzichtet). Wir können somit die Teststatistik berechnen durch

$T=\frac{25,61-21,23}{1,43}=\frac{4,38}{1,43}\approx 3,06.$

Im nächsten Schritt wird die Testentscheidung getroffen: Wir betrachten wieder drei Möglichkeiten, um über die Ablehnung der Nullhypothese zu entscheiden.
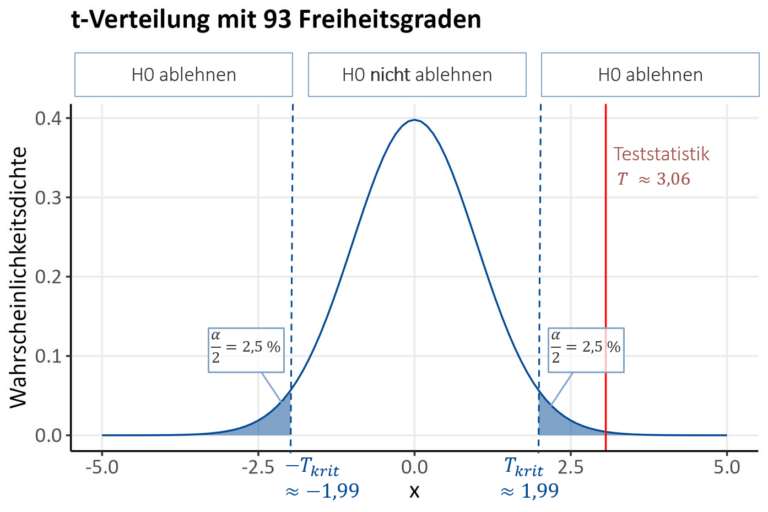
Als erstes vergleichen wir die Teststatistik mit dem kritischen Wert: Wir lehnen die Nullhypothese ab, wenn sich der berechnete Wert der Teststatistik $T$ im Ablehnungsbereich befindet. Es handelt sich bei der t-Verteilung um eine um 0 zentrierte, symmetrische Verteilung mit positiven und negativen Werten. Da wir einen zweiseitigen Test durchführen (wir betrachten eine Unterschiedshypothese, bei der beide Richtungen des Unterschieds relevant sind), ist der Ablehnungsbereich auch auf beide Seiten der Verteilung verteilt (siehe Grafik). Die Teststatistik liegt also im Ablehnungsbereich, wenn sie entweder noch kleiner als der negative kritische Wert oder größer als der positive kritische Wert $T_{krit}$ ist. Die kritischen Werte unterscheiden sich aufgrund der Symmetrie der t-Verteilung nur durch ihr Vorzeichen. Somit kann man die beiden Möglichkeiten auch zusammenfassen durch $|T|>T_{krit}$ (man vergleicht also die Teststatistik als positive Zahl mit dem kritischen Wert).

Wie lässt sich nun der kritische Wert $T_{krit}$ ermitteln? Der kritische Wert ist das $(1-\frac{\alpha}{2})$ –Quantil der t-Verteilung mit der spezifischen Anzahl an Freiheitsgraden $df$ . Da der Ablehnungsbereich wie gesagt auf beide Seiten der Verteilung aufgeteilt ist, teilen wir auch $\alpha$ durch zwei, wir erlauben jeweils die Hälfte des Fehlers 1. Art auf beiden Seiten. Die Anzahl an Freiheitsgraden lässt sich für die t-Verteilung berechnen durch $df= n_1+ n_2-2$ (also die Gesamtfallzahl minus zwei). Zusammengefasst lehnen wir die Nullhypothese also ab, wenn $|T|>t(1-\frac{\alpha}{2}, df)$ .

Beispiel "Blutdrucksenker"

Für unser Beispiel vergleichen wir also den Betrag der Teststatistik $|T|=3,06$ mit dem 97,5%-Quantil der t-Verteilung bei $df=49+46-2=93$ Freiheitsgraden, also $t(0,975; 93)\approx 1,99$ . Da

$|T|=3,06>1,99 \approx t(0,975; 93)$

können wir die Nullhypothese ablehnen.

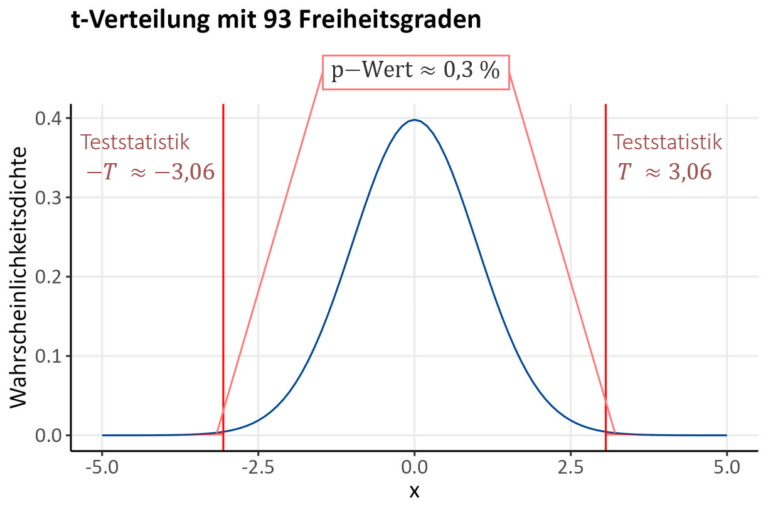
Die zweite Möglichkeit ist es, den $p$ -Wert mit dem festgelegten Signifikanzniveau zu vergleichen. Ist der $p$ -Wert kleiner als das Signifikanzniveau $\alpha$ , können wir die Nullhypothese ablehnen. Da wir einen zweiseitigen t-Test durchführen, ergibt sich der $p$ -Wert aus der Summe der Flächen unter der Kurve der t-Verteilung links und rechts von der positiven und negativen Ausprägung der Teststatistik.

Beispiel "Blutdrucksenker"

Hier ergibt sich $p\approx 0,003=0,3\%$ , was ein sehr kleiner Wert ist. Deshalb sind in der folgenden Grafik die Flächen unter der Kurve (in rot gefärbt) nicht sehr gut zu erkennen.

$p\approx 0,003<0,05= \alpha$

können wir auch hier die Nullhypothese ablehnen.

Als letztes wollen wir die Testentscheidung mithilfe des aufgestellten Konfidenzintervalls für den Schätzer der Mittelwertsdifferenz $\widehat{MD}$ treffen. Da es sich um einen Differenzschätzer handelt, erfolgt die Ablehnung, wenn unser aus den Daten ermitteltes Konfidenzintervall für $\widehat{MD}$ die 0 nicht enthält.

Beispiel "Blutdrucksenker"

Wir wollen also ein Konfidenzintervall für den Differenzschätzer ermitteln. Wir nutzen die Formel, die ihr im Abschnitt Konfidenzintervalle für Differenzschätzer kennengelernt habt:

$(1-\alpha)-KI_{\text{wahrer Wert}}=[Differenzschätzer \pm t(1-\frac{\alpha}{2}; df)\cdot SE_{\text{wahrer Wert}}].$

Vielleicht ist euch aufgefallen, dass an dieser Stelle ein anderes Quantil für das Konfidenzintervall verwendet wurde als bisher. Dies liegt daran, dass der t-Test auf der t-Verteilung beruht und somit das Quantil dieser Verteilung und nicht das Quantil der Standardnormalverteilung (siehe t-Test vs. z-Test) genutzt wird. Es ergibt sich für unseren konkreten Fall für die Mittelwertsdifferenz und mit $\alpha=5\%$ , $t(1-\frac{\alpha}{2}; df)\approx 1,99$ und $SE_{MD}\approx 1,43$

$95\%-KI_{MD}=[\widehat{MD}\pm 1,99 \cdot SE_{MD}]$

$=[4,38-1,99\cdot 1,43;\text{ } 4,38+1,99\cdot 1,43]$

$=[1,53;\text{ } 7,23].$

Unser Konfidenzintervall für die geschätzte Mittelwertsdifferenz enthält die Null nicht, sodass wir die Nullhypothese ablehnen können.

Beispiel "Blutdrucksenker"

Es folgt also über jeden der drei thematisierten Wege die Ablehnung der Nullhypothese. Die Ergebnbisse sind in der folgenden Grafik (Abb. 9) zusammengefasst.

Der letzte Schritt ist es, die Ergebnisse in Bezug zur Fragestellung, also auf inhaltlicher Ebene, zu interpretieren.

Beispiel "Blutdrucksenker"

Wir können bei Ablehnung der Nullhypothese folglich auf einen signifikanten Mittelwertunterschied der Blutdruckdifferenzen zwischen der Interventionsgruppe mit der neuen Intervention und der Kontrollgruppe mit der Standardtherapie schließen.

ACHTUNG: Es muss beachtet werden, dass aufgrund des zweiseitigen Tests auf eine Unterschiedshypothese anhand des $p$ -Werts erstmal nicht auf die Richtung des Unterschieds geschlossen kann. Es kann lediglich geschlossen werden, dass signifikant unterschiedliche Ergebnisse aufgetreten sind. Für die Richtung betrachtet man dann den Effektschätzer und / oder das Konfidenzintervall.

Zusatzwissen

Weitere Arten des t-Tests

Weitere Arten des t-Tests sind der t-Test für abhängige Stichproben und der Ein-Stichproben t-Test.

Der t-Test für abhängige Stichproben wird, wie der Name schon sagt, genutzt, um Mittelwerte zwischen zwei voneinander abhängigen Gruppen zu vergleichen. Zwei Gruppen können z. B. abhängig voneinander sein, wenn es sich um die gleichen Versuchspersonen handelt, deren Daten zu unterschiedlichen Zeitpunkten erhoben werden. In unserem Beispiel könnte z. B. die Blutdruck senkende Wirkung der neuen Intervention untersucht werden, indem geprüft wird, ob sich die Blutdruckmesswerte derselben Patient:innen vor und nach der neuen Intervention signifikant voneinander unterscheiden.

Der Ein-Stichproben t-Test ist dann geeignet, wenn die betrachtete Stichprobe gegen einen festen Wert verglichen werden soll. Ist es z. B. von Interesse, ob ein gewisser Grenzwert bei der Differenz zwischen dem Blutdruck nach und vor der Intervention überschritten wird, kann der Ein-Stichproben t-Test hilfreich sein. Als Alternativhypothese wird formuliert, dass die Differenz größer als dieser festgelegte Grenzwert ist, was bestenfalls durch Ablehnung der Nullhypothese geschlossen werden kann.

Log Rank-Test

Im Abschnitt zu den deskriptiven grafischen Methoden, haben wir bereits gesehen, dass es interessant sein kann, zwei Kaplan-Meier-Kurven (z. B. pro Behandlungsgruppe) für (teilweise zensierte) Ereigniszeitdaten miteinander zu vergleichen. Der Log Rank-Test ist ein statistischer Test, um genau das zu tun: Er hilft uns, zu überprüfen, ob sich die Kaplan-Meier-Kurven der Ereigniszeitdaten zweier Gruppen statistisch signifikant voneinander unterscheiden oder nicht. Dabei geht es nicht um einen einzelnen konkreten Zeitpunkt (z. B. das Studienende), sondern um den Vergleich über den gesamten Zeitraum hinweg.

Der Log Rank-Test ist ein Standardverfahren in der Analyse von Ereigniszeitdaten, besonders da er zensierte Daten angemessen in der Analyse berücksichtigt. Eine weitere Methode im Zusammenhang mit Ereigniszeitdaten, die für die Untersuchung des Einflusses einer metrischen Variablen auf eine Variable auf der Ereigniszeitskala geeignet ist, ist die Cox-Regression (eine spezielle Form der Regressionsanalyse), auf die im Rahmen des EpiBioManuals allerdings nicht weiter eingegangen werden soll. Ihr Vorteil ist, dass in der Cox-Regression mehrere Einflussvariablen und andere Kovariablen berücksichtigt werden können, die die Ereigniszeitvariable beeinflussen könnten.

Wir wollen uns nun anschauen, wie man einen Log Rank-Test durchführt. Wir gehen dabei nicht ins Detail – es reicht, das grobe Konzept des Tests zu verstehen.

Beispiel "Blutdrucksenker"

Wir wollen uns an dem gängigen Ablauf statistischer Tests orientieren und damit die Grundschritte eines Log Rank-Tests für unsere Beispielstudie durchführen. Die Fragestellung ist, ob sich die Zeit, bis der Blutdruck in den Normbereich gesunken ist (zeit_BD_norm) in der Interventions- und der Kontrollgruppe (Gruppenzuteilung) unterscheidet.

Beispiel "Blutdrucksenker"

Wir stellen im ersten Schritt geeignete Hypothesen für unsere Beispielstudie auf:

$H0$ : Die betrachteten Gruppen (Interventions- und Kontrollgruppe) haben eine identische Kaplan-Meier-Kurve der Ereigniszeitvariablen zeit_BD_norm.
$H1$ : Die betrachteten Gruppen weisen unterschiedliche Kaplan-Meier-Kurven der Ereigniszeitvariablen zeit_BD_norm auf.

Beispiel "Blutdrucksenker"

Wir legen wie gehabt ein Signifikanzniveau $\alpha=5\%$ fest.

Beispiel "Blutdrucksenker"

Wir wollen den Zusammenhang der nominalen Variablen der Gruppenzuteilung mit der Ereigniszeitvariablen zeit_BD_norm untersuchen. Damit bietet sich der hier thematisierte Log Rank-Test an.

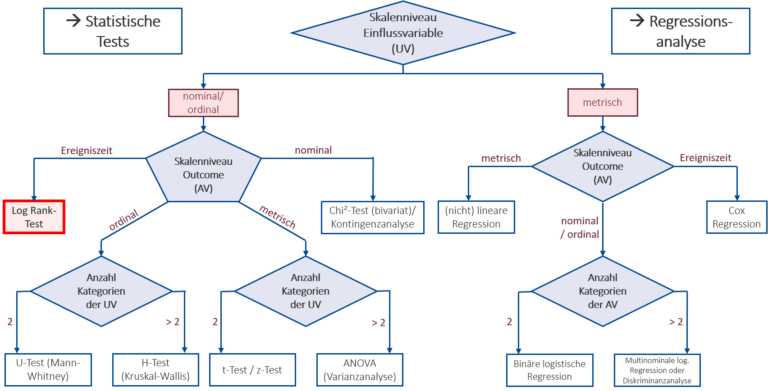
Eine Voraussetzung, die erfüllt sein muss, damit ein Log Rank-Test durchgeführt werden kann, ist die Annahme, dass das Hazard Ratio über den gesamten Zeitraum hinweg konstant bleiben muss (man sagt auch proportional hazards). Auf unser Beispiel bezogen bedeutet das, dass das Verhältnis der Wahrscheinlichkeiten (Hazardraten), mit dem Blutdruck in den Normbereich zu sinken, im Verlauf der Studie konstant ist. Ob das in der Realität der Fall ist, ist zu bezweifeln – wir gehen aber aus Gründen der Vereinfachung an dieser Stelle davon aus.

Wie genau beim Log Rank-Test die Teststatistik ermittelt wird, werden wir hier nicht weiter thematisieren.

Beispiel "Blutdrucksenker"

Im nächsten Schritt werden nach der Planungsphase die Ereigniszeitdaten über den gesamten, vorher definierten Zeitraum erhoben.

Wir haben die Teststatistik für unser Beispiel mithilfe statistischer Software ermittelt: $T=6,11$ .

Der Log Rank-Test basiert auch auf der Chi-Quadrat-Verteilung, sodass der kritische Wert das $(1-\alpha)$ –Quantil der Chi-Quadrat-Verteilung mit $df = (k-1)$ Freiheitsgraden ist, wobei $k$ die Anzahl an betrachteten Gruppen angibt. Wir schauen uns hier also das 95 %- Quantil der Chi-Quadrat-Verteilung mit 1 Freiheitsgrad an und es ergibt sich $T_{krit}\approx 3,84$ . Der $p$ -Wert liegt bei $p=0,01$ .

Beispiel "Blutdrucksenker"

Im fünften Schritt treffen wir die Testentscheidung. Da die Teststatistik größer ist als der kritische Wert, also

$T=6,11 > 3,84 \approx T_{krit}$ ,

lehnen wir die Nullhypothese ab.
Außerdem ist der $p$ -Wert kleiner als das festgelegte Signifikanzniveau, also

$p=0,01 < 0,05 = \alpha$ ,

sodass wir auch damit die Nullhypothese ablehnen können.

Beispiel "Blutdrucksenker"

Als letztes gilt es die Ergebnisse zu interpretieren. Die Ablehnung der Nullhypothese bedeutet, dass wir auf die Alternativhypothese schließen können. Dementsprechend unterscheiden sich die Kaplan-Meier-Kurven der Ereigniszeitdaten zwischen der Interventions- und der Kontrollgruppe signifikant voneinander.

Zusammenfassung

Der Ablauf eines statistischen Tests kann somit durch insgesamt 6 Schritte zusammengefasst werden:

Hypothesen formulieren
Signifikanzniveau $\alpha$ festlegen
Auswahl eines geeigneten Testverfahrens mit der entsprechenden Teststatistik

Daten sammeln

Teststatistik bzw. $p$ -Wert berechnen
Testentscheidung treffen
Ergebnisse interpretieren

Wird der statistische Test im Rahmen einer gesamten wissenschaftlichen Studie durchgeführt, sollten die Punkte 1-3 bereits in der Planung der Studie genau festgelegt und dokumentiert werden. Die Datensammlung erfolgt im Schritt der Durchführung der Studie, während die Punkte 4 bis 6 zum Abschnitt der Auswertung der Studienergebnisse gehören, in dem wir uns jetzt auch mit diesem EpiBioManual-Abschnitt befinden.

Zum Aufstellen passender Hypothesen

Download der Tabelle in Abb. 11 als PDF

Zur Festlegung des Signifikanzniveaus (meist $\alpha=5\%$ )²

Testentscheidung vs. Realität (mögliche Fälle und ihre jeweilige Wahrscheinlichkeit)
		Realität
		$H0$ wahr	$H1$ wahr
Testentscheidung für …	$H0$	Richtig (Grad an gewünschter Sicherheit): $1-\alpha$	Fehler 2. Art: $\beta$
Testentscheidung für …	$H1$	Fehler 1. Art: $\alpha$	Richtig (Power): $1-\beta$

Zur Auswahl eines geeigneten Testverfahrens

Download der Abb. 12 in Listenform als PDF

Zur Berechnung der Teststatistik

Kurzzusammenfassung der hier thematisierten Tests:

	Chi-Quadrat-Test	t-Test	Log Rank-Test
Teststatistik	$X^2=a_{diff}+b_{diff} +c_{diff}+d_{diff}$ mit $x_{diff}=\frac{(x-x_{erw})^2}{x_{erw}}$	$T=\frac{\overline{x}_l-\overline{x}_k}{SE_{MD}} =\frac{\widehat{MD}}{SD_{MD}}$	Hier nicht weiter thematisiert
Kritischer Wert	$(1-\alpha)$ –Quantil der Chi²-Verteilung mit $df=(k-1) \cdot (l-1)$	$(1-\frac{\alpha}{2})$ –Quantil der t-Verteilung mit $df=n_l + n_k - 2$	$(1-\alpha)$ –Quantil der Chi²-Verteilung mit $df=(k-1)$

Zum Treffen der Testentscheidung

Wir lehnen die Nullhypothese ab, wenn…

… die Teststatistik im Ablehnungsbereich liegt, also größer ist als der kritische Wert:
- Chi-Quadrat-Test: Teststatistik größer ist als der kritische Wert: $T>T_{krit}$
- Zweiseitiger t-Test: Teststatistik ist kleiner/größer als der negative/positive kritische Wert: $T<-T_{krit}$ oder $T>T_{krit}$ , oder geschrieben als $|T|>|T_{krit}|$
… der $p$ -Wert kleiner als das Signifikanzniveau ist: $p<\alpha$
… das Konfidenzintervall für den betrachteten Differenzschätzer die Null nicht enthält:
$0 \not\in (1-\alpha)\text{-}KI_{\text{wahre Differenz}}$
bzw.
… das Konfidenzintervall für den betrachteten Verhältnisschätzer die Eins nicht enthält:
$1 \not\in (1-\alpha)\text{-}KI_{\text{wahres Verhältnis}}$

Weitere Themen im Zusammenhang mit statistischen Tests

Was passiert, wenn das Ergebnis nicht signifikant ist?

In unserem bisherigen Beispiel war der Unterschied zwischen den betrachteten Gruppen so groß, dass die durchgeführten Tests unabhängig von der Definition des Behandlungserfolgs zu signifikanten Ergebnissen bezüglich des Gruppenunterschieds geführt haben. In der Praxis ist dies allerdings häufig nicht der Fall. Wie interpretieren wir ein nicht signifikantes Ergebnis? Ein nicht signifikantes Ergebnis kann zwei Ursachen haben: Entweder gibt es keinen Unterschied oder der Unterschied lässt sich durch unseren Test aufgrund einer zu kleinen Stichprobe nicht statistisch absichern (siehe dazu Fallzahlplanung).

ACHTUNG:

„Absence of evidence is not evidence of absence.“ (Carl Sagan)

Können wir die Nullhypothese nicht ablehnen, bedeutet das nicht im Umkehrschluss, dass wir sie jetzt annehmen dürfen: keine Ablehnung = kein signifikantes Ergebnis = kein bestätigter Zusammenhang / Unterschied. In unserem Beispiel hätte ein nicht signifikantes Ergebnis also nicht unbedingt bedeutet, dass beide Behandlungsgruppen äquivalente Entwicklungen zeigen, sondern lediglich, dass es keinen signifikanten Unterschied zwischen den Gruppen gibt. Wäre es das Ziel unserer Studie gewesen, genau diese Äquivalenz zwischen den Gruppen statistisch abzusichern, hätten wir Forschungshypothese anders formulieren müssen. Mithilfe einer Äquivalenzhypothese kann z. B. durch Ablehnung der Nullhypothese statistisch abgesichert werden, dass beide Gruppen äquivalente Ergebnisse aufweisen. Ihr seht also, dass es stets von großer Bedeutung ist, vor Studienbeginn genau zu überlegen, was untersucht werden soll und dementsprechend die geeigneten Hypothesen aufzustellen. Im besten Fall könnt ihr dann durch Ablehnung der Nullhypothese und das Schließen auf die Alternativhypothese genau das statistisch absichern, was ihr zeigen wolltet. Im Nachhinein sollten diese vor Studienbeginn aufgestellten Hypothesen niemals geändert werden, um doch noch signifikante Ergebnisse zu erzeugen!

Ist das Ergebnis nicht signifikant, sollte auch das unbedingt berichtet werden, denn auch ein nicht signifikantes Ergebnis ist ein Ergebnis. In der Forschungspraxis ist es ein großes Problem, dass oft ein verzerrtes Bild über bestimmte Sachverhalte entsteht, da lieber signifikante Ergebnisse veröffentlicht und nicht signifikante Ergebnisse häufig als „unwichtig“ oder „uninteressant“ unter den Teppich gekehrt werden. Man spricht dabei auch von Publikationsbias. Dies kann z. B. zur Folge haben, dass die Wirksamkeit von neuen Therapien überschätzt wird und diese auf Basis verzerrter Metaanalysen im Rahmen der evidenzbasierten Medizin trotzdem zur Therapieempfehlung wird.
Ein Extrembeispiel: In 9 nicht veröffentlichten Studien konnte keine signifikante Wirksamkeit eines neuen Medikaments gezeigt werden. In der einzig veröffentlichten Studie wurde die Wirkung gezeigt und das neue Medikament als Wundermittel gefeiert. Ihr seht sicherlich die Gefahr in dieser Vorgehensweise.

Zusammengefasst: Die Fragestellung und spezifische Forschungshypothesen sollten vor Studienbeginn genau definiert und nicht mehr geändert werden. Auch nicht signifikante Ergebnisse liefern einen Beitrag und sollten berichtet und, wenn irgendwie möglich, veröffentlicht werden. Außerdem sollten Studien am besten durch unabhängige Institutionen ohne Interessenskonflikte durchgeführt werden.

Signifikanz vs. Relevanz

Statistische Signifikanz alleine gibt keine Auskunft darüber, ob das Ergebnis auch Relevanz für die (klinische) Praxis hat. Vielleicht ist der beobachtete Effekt z. B. zwar signifikant, aber so klein, dass er keinerlei praktischen Nutzen aufweist. Auch andersherum kann ein statistisch nicht signifikanter Effekt aufgrund der großen Effektstärke in der Praxis trotzdem relevant sein. Ab wann ein Ergebnis relevant ist, hängt davon ab, wie man den Begriff „Relevanz“ definiert, was wiederum vom Fachgebiet und der betrachteten Fragestellung abhängt. Somit wird die statistische Signifikanz auf Basis des $p$ -Werts bewertet und die Relevanz anhand der Stärke des Effekts von Fachleuten aus der (klinischen) Praxis beurteilt.

Beispiel "Blutdrucksenker"

Wir betrachten wieder unser Beispiel zum Blutdruck senkenden Medikament, wo ein t-Test für unabhängige Stichproben durchgeführt wurde, um Mittelwertunterschiede zwischen den Behandlungsgruppen zu untersuchen. Ein/e Mediziner:in hat dabei vorher festgelegt, dass ein systolischer Blutdruckunterschied von mehr als 4 mmHg zwischen den Behandlungsgruppe als klinisch relevant gilt. Somit legen wir die sogenannte Relevanzgrenze auf $RG= 4 \text{ mmHg}$ . Wir wollen uns nun mithilfe der Abbildung 13 die verschiedenen möglichen Testergebnisse dieses t-Tests anschauen. Wenn wir ein Konfidenzintervall für die geschätzte Mittelwertsdifferenz aufstellen und dieses die Null enthält, spricht das, wie im Abschnitt zum t-Test erklärt, dafür, dass kein signifikanter Mittelwertsunterschied zwischen den Gruppen vorliegt. Das ist in Abb. 13 bei (a) der Fall. Da der Fall (a) zusätzlich auch unter der Relevanzgrenze liegt, sind die Ergebnisse weder signifikant noch relevant. In Fall (b) konnten zwar signifikante Ergebnisse berichtet werden, allerdings waren die beobachteten Ergebnisse klinisch nicht relevant. Fall (c) ist zwar nicht signifikant, aber kann für die medizinische Praxis trotzdem von Bedeutung sein, da die Relevanzgrenze durch den Punktschätzer für die Mittelwertsdifferenz überschritten wurde und sollte in weiteren Studien untersucht werden. Der Fall (d) ist sowohl statistisch signifikant als auch klinisch relevant und damit das Ergebnis, das man sich in Studien zum Nachweis der Wirksamkeit wünscht.
In unserem konkreten Beispiel lagen signifikante Ergebnisse auf Basis eines kleinen $p$ -Werts vor und zusätzlich war die geschätzte Mittelwertsdifferenz bei $\widehat{MD}\approx 4,38$ und damit größer als die Relevanzgrenze $RG= 4 \text{ mmHg}$ . Wir können also von statistisch signifikanten und klinisch relevanten Ergebnissen sprechen.

Multiplizität

Das Multiplizitätsproblem wird dann relevant, wenn wir mehrere zusammenhängende statistische Tests im Rahmen einer Studie hintereinander durchführen (sogenanntes multiples Testen). Ihr wisst bereits, dass wir mit dem Signifikanzniveau $\alpha$ die gerade noch tolerierbare Wahrscheinlichkeit für einen Fehler 1. Art (also eine falsch-signifikante Entscheidung zugunsten der Alternativhypothese) festlegen. Wenn wir nun mehrere Tests hintereinander durchführen und jedes Mal das Risiko besteht, diesen Fehler zu begehen, erhöht sich die Wahrscheinlich für mindestens ein falsch-signifikantes Ergebnis unter allen Tests zunehmend. Man spricht in diesem Fall auch von einer Inflation des $\alpha$ -Fehlers. Guck dir z. B. Tabelle 2 an, wenn wir das typisch verwendete Signifikanzniveau $\alpha = 5\%$ festlegen. Bereits bei 10 Tests liegt das Risiko für mindestens ein falsches Ergebnis bei $40\%$ .

Tab. 2: Wahrscheinlichkeiten für mindestens ein falsch-signifikantes Ergebnis bei unterschiedlicher Anzahl an Tests
Anzahl Tests	Wahrscheinlichkeit
1	0,05 = 5%
2	0,10 = 10%
3	0,14 = 14%
5	0,23 = 23%
10	0,40 = 40%

Ihr fragt euch sicherlich, warum man in der Praxis so viele statistische Tests hintereinander durchführen sollte, oder? Dies ist tatsächlich gar nicht so unrealistisch, wenn in einer Studie beispielsweise mehrere Endpunkte, Zeitpunkte oder verschiedene (Sub-)Gruppen untersucht werden sollen. Dies wäre ohne die eben genannte Multiplizitätsproblematik einfach durch mehrere einzelne hintereinander durchgeführte statistische Tests möglich. Auch wenn bereits vor Studienende das Interesse besteht, Zwischenanalysen durchzuführen („ich wollte nur schon mal reingucken, ob der Versuch in die richtige Richtung läuft.“), führt das zu einer Inflation des $\alpha$ -Fehlers. Besonders in Zeiten, wo solche Tests sehr schnell und einfach mithilfe statistischer Software durchzuführen sind, sind Anwender:innen oft geneigt, immer mehr und mehr Tests durchzuführen und so teilweise sogar nach signifikanten Ergebnissen zu suchen.

Um das Problem zu vermeiden, sollte in der Studienplanung genau überlegt werden, was die Hauptfragestellung ist. Der zugehörige Test ist dann der einzige konfirmatorische Test. Auch für sekundäre Endpunkte, verschiedene Zeitpunkte usw. können statistische Tests durchgeführt werden. Damit werden aber keine Testentscheidungen getroffen, sondern die $p$ -Werte dienen als deskriptive Kenngrößen, die entsprechend interpretiert werden (nicht, ob größer oder kleiner als $\alpha$ , sondern je kleiner, desto eher spricht das für einen Unterschied, je größer, desto weniger). Wenn es primär mehr als eine Hypothese von Interesse ist, gibt es Methoden zur Adjustierung des $\alpha$ -Fehlers, wie z. B. die Bonferroni-Korrektur. Dabei wird das Signifikanzniveau anteilig auf alle Tests aufgeteilt, indem $\frac{\alpha}{\text{Testanzahl}}$ berechnet wird, sodass die Wahrscheinlichkeit für einen $\alpha$ -Fehler insgesamt wieder bei $5 \%$ liegt. Es gibt auch noch andere Methoden zur Adjustierung, auf die im Rahmen dieser Vorlesung aber nicht weiter eingegangen werden soll.

Fallzahlplanung

Je größer die Stichprobe ist, desto wahrscheinlicher ist es signifikante Effekte zu finden. Wenn du dir z. B. nochmal die Berechnungsformel für die Teststatistik bei einem t-Test anschaust, siehst du, dass im Nenner der Standardfehler genutzt wird, der bei steigender Fallzahl immer kleiner wird (schaue dir nochmal die Formel zur Berechnung des Standardfehlers an). Wird der Standardfehler immer kleiner, lässt dies die Teststatistik größer werden, da der Standardfehler im Nenner des Bruchs steht. Somit wird bei steigender Fallzahl, die Teststatistik immer größer. Das kann dazu führen, dass bereits kleinste und praktisch vielleicht unerhebliche Abweichungen von der Nullhypothese als statistisch signifikante Effekte eingestuft werden. So werden in der Praxis teilweise statistische Tests „missbraucht“, indem nachträglich z. B. nochmal die Fallzahl erhöht wird, um signifikante Ergebnisse zu erzeugen. Genau aus diesem Grund muss dringend a priori, also vor Durchführung der Studie, eine bindende Fallzahlplanung stattfinden. Trotzdem thematisieren wir in diesem EpiBioManual die Fallzahlplanung erst an dieser Stelle und nicht bereits im Abschnitt zur Studienplanung, da ihr erst die Konzepte des statistischen Tests kennenlernen musstet, um die Formel zur Berechnung der benötigten Fallzahl zu verstehen. Zu jedem statistischen Test gibt es eine eigene Fallzahlplanungsformel, die angewendet werden kann, um die benötigte Fallzahl zu berechnen. Für einen t-Test berechnet sich die Fallzahl z. B. wie folgt:

$n_{Gruppe}=\frac{2\cdot( t_{1-\frac{\alpha}{2}}+t_{1-\beta,df})^2}{(\frac{\Delta}{\sigma})^2}$

Eine geeignete Fallzahl ist somit abhängig vom jeweiligen Testdesign (z. B. handelt es sich um abhängige oder unabhängige Stichproben?), dem festgelegten Signifikanzniveau , der angestrebten Power des Tests , den erwarteten bzw. relevanten Unterschied (d. h. die Fallzahlplanung beachtet auch den oben betrachteten Unterschied zwischen Relevanz und Signifikanz) und die Variabilität . Nimmt der/die Testanwender:in ein größeres Risiko für den Fehler 1. Art in Kauf oder wird der untersuchte erwartete Gruppenunterschied immer größer, sind weniger Versuchspersonen pro Gruppe notwendig, um einen signifikanten Effekt zu zeigen. Hingegen benötigen wir mehr Versuchspersonen pro Gruppe, wenn wir eine größere Power anstreben wollen oder die Variabilität in den Daten als hoch eingestuft wird. In Tabelle 3 sind die Zusammenhänge dieser Größen mit der Fallzahl pro Gruppe dargestellt.

Tab. 3: Einfluss der Änderung bestimmter Testgrößen auf die angemessene Fallzahl (pro Gruppe)
Änderung	Fallzahl pro Gruppe
Signifikanzniveau $\alpha$ steigt ▲	sinkt ▼
erwartete Mittelwertsdifferenz $\Delta$ steigt ▲	sinkt ▼
angestrebte Power $1-\beta$ steigt ▲	steigt ▲
erwartete Standardabweichung $\sigma$ steigt ▲	steigt ▲

Beispiel "Blutdrucksenker"

Für unser Beispiel haben wir aus Einfachheit die Stichprobengröße auf 100 Versuchspersonen festgelegt. Besser wäre es gewesen, hätten wir die benötigte Fallzahl für den t-Test anhand der oben genannten Formel a priori ermittelt und im Studienprotokoll dokumentiert. Wir hätten, wie auch im Rahmen des Tests, das Signifikanzniveau auf $\alpha=5 \%$ festgelegt und damit $t_{1-\frac{\alpha}{2},df}\approx 1,96$ und für eine gewünschte Power von 0,9 das Quantil $t_{1-\beta,df}\approx 1,28$ erhalten. Der erwartete Mittelwertsunterschied zwischen den beiden Behandlungsgruppen und die Standardabweichung als Annahme für die Variabilität der Ergebnisse wurde von einem/r Mediziner:in vor Studienbeginn angesetzt: Wir gehen von $\Delta=4 \text{ mmHg}$ und $\sigma=6 \text{ mmHg}$ aus. Damit ergibt sich eine optimale Fallzahl von $n_{Gruppe}\approx \frac{2\cdot (1,96+1,28)^2}{(\frac{4}{6})^2}\approx 47,24$ pro Gruppe, sodass wir mit unseren insgesamt 100 Versuchspersonen gar nicht so weit von der optimalen Fallzahl entfernt liegen.

LITERATURVERZEICHNIS

Die Inhalte dieser Seite sind angelehnt an:

Weiß, Christel (2013): Prinzip eines statistischen Test. In: Christel Weiß (Hg.): Basiswissen Medizinische Statistik. Mit 20 Tabellen. 6., überarbeitete Auflage. Berlin, Heidelberg: Springer (Springer-Lehrbuch), S. 161-177, Kapitel 9, insbesondere 9.1.4, 9.2.4 und 9.2.6.

Weiß, Christel (2013): Lagetests. In: Christel Weiß (Hg.): Basiswissen Medizinische Statistik. Mit 20 Tabellen. 6., überarbeitete Auflage. Berlin, Heidelberg: Springer (Springer-Lehrbuch), S. 179-197, Kapitel 10.1.

Weiß, Christel (2013): Tests zum Vergleich von Häufigkeiten. In: Christel Weiß (Hg.): Basiswissen Medizinische Statistik. Mit 20 Tabellen. 6., überarbeitete Auflage. Berlin, Heidelberg: Springer (Springer-Lehrbuch), S. 199-216, Kapitel 11.1.1 und 11.1.7.

Schumacher, M.; Olschewski, M.(2008): Analyse von Ereigniszeiten – Teil I. In: Methodik klinischer Studien. Methodische Grundlagen der Planung, Durchführung und Auswertung. Martin Schumacher, Gabi Schulgen (Hg.), 3. Aufl., Springer Verlag, S. 77-94, Kapitel 5.3.

Außerdem:

Caputo, A.; Graf, E. (2008): Planung einer klinischen Studie: Wie viele Patienten sind notwendig? In: Martin Schumacher und Gabi Schulgen/Kristiansen (Hg.): Methodik klinischer Studien. Berlin, Heidelberg: Springer Berlin Heidelberg (Statistik und ihre Anwendungen), S. 171–193, Kapitel 10.

Du Prel, J.-B.; Hommel, G.; Röhrig, B.; Blettner, M.(2009): Confidence interval or p-value?: part 4 of a series on evaluation of scientific publications. In: Deutsches Arzteblatt international 106 (19), S. 335–339. DOI: 10.3238/arztebl.2009.0335.

Schwarzer, G., Timmer, A., Galandi, D., Antes, G., Schumacher, M. (2008). Meta-Analyse randomisierter klinischer Studien, Publikationsbias und evidenzbasierte Medizin. In: Methodik klinischer Studien. Methodische Grundlagen der Planung, Durchführung und Auswertung. Martin Schumacher, Gabi Schulgen (Hrg.), 3. Aufl., Springer Verlag, S. 129-160, Kapitel 8.

Fußnoten

1
Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2023), Universitätsklinikum Hamburg-Eppendorf.
2
Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2023), Universitätsklinikum Hamburg-Eppendorf.
3
Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2023), Universitätsklinikum Hamburg-Eppendorf.
4
Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2023), Universitätsklinikum Hamburg-Eppendorf.
5
Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2023), Universitätsklinikum Hamburg-Eppendorf.
6
Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2023), Universitätsklinikum Hamburg-Eppendorf.
7
Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2023), Universitätsklinikum Hamburg-Eppendorf.
8
Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2023), Universitätsklinikum Hamburg-Eppendorf.
9
Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2023), Universitätsklinikum Hamburg-Eppendorf.
10
Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2023), Universitätsklinikum Hamburg-Eppendorf.
11
Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2023), Universitätsklinikum Hamburg-Eppendorf.
12
Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2023), Universitätsklinikum Hamburg-Eppendorf.
13
Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2023), Universitätsklinikum Hamburg-Eppendorf.
14
Lisa Holstein, Christian Wiessner, Antonia Zapf (Institut für Medizinische Biometrie und Epidemiologie) (2023), Universitätsklinikum Hamburg-Eppendorf angelehnt an Grafik 2 in Du Prel, Jean-Baptist; Hommel, Gerhard; Röhrig, Bernd; Blettner, Maria (2009): Confidence interval or p-value?: part 4 of a series on evaluation of scientific publications. In: Deutsches Arzteblatt international 106 (19), S. 335–339. DOI: 10.3238/arztebl.2009.0335.